
【题目】如图,![]() ,点
,点![]() 为直线
为直线![]() 上一定点,
上一定点,![]() 为直线
为直线![]() 上的动点,在直线
上的动点,在直线![]() 与
与![]() 之间且在线段
之间且在线段![]() 的右方作点
的右方作点![]() ,使得
,使得![]() .设
.设![]() 为锐角).
为锐角).
(1)求![]() 与
与![]() 的和;(提示过点
的和;(提示过点![]() 作
作![]()
(2)当点![]() 在直线
在直线![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(3)当点![]() 在直线
在直线![]() 上运动的过程中,若
上运动的过程中,若![]() 平分
平分![]() ,
,![]() 也恰好平分
也恰好平分![]() ,请求出此时
,请求出此时![]() 的值
的值
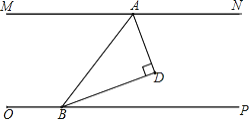
【答案】(1)∠NAD+∠PBD=90°;(2)见解析;(3)30°
【解析】
(1)过点D作EF∥MN,根据平行于同一条直线的两直线平行,可得EF∥OP,从而得出∠NAD=∠ADE,∠PBD=∠BDE,然后根据垂直的定义可得∠ADE+∠BDE=90°,然后利用等量代换即可得出结论;
(2)将(1)的结论变形可得∠PBD=90°-∠NAD,然后根据平角的定义和等量代换即可证出结论;
(3)根据角平分线的定义可得∠NAD=![]() ,∠NAB=2
,∠NAB=2![]() ,∠OBD=2∠OBA,然后根据平行线的性质可得∠OBA=∠NAB=
,∠OBD=2∠OBA,然后根据平行线的性质可得∠OBA=∠NAB=![]() ,从而求出∠OBD=
,从而求出∠OBD=![]() ,最后根据(2)的结论列方程即可求出结论.
,最后根据(2)的结论列方程即可求出结论.
解:(1)过点D作EF∥MN,如下图所示
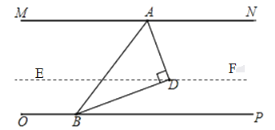
∵![]()
∴EF∥OP
∴∠NAD=∠ADE,∠PBD=∠BDE
∵![]()
∴∠ADB=90°
∴∠ADE+∠BDE=∠ADB=90°
∴∠NAD+∠PBD=90°
(2)∵∠NAD+∠PBD=90°
∴∠PBD=90°-∠NAD
∵∠OBD+∠PBD=180°,
∴∠OBD+90°-∠NAD=180°
∴![]() ;
;
(3)∵![]() 平分
平分![]() ,
,![]() 也恰好平分
也恰好平分![]() ,
,![]()
∴∠NAD=![]() ,∠NAB=2
,∠NAB=2![]() ,∠OBD=2∠OBA
,∠OBD=2∠OBA
∵![]()
∴∠OBA=∠NAB=![]()
∴∠OBD=![]()
由(2)知![]()
即![]()
解得:![]()


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】某班购买一些乒乓球和乒乓球拍,了解信息如下:甲、乙两家商店出售同种品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元.经洽谈,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折出售,该班需球拍5副,乒乓球若干盒(不少于5盒)问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示).
(2)如果要购买15盒乒乓球,请你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
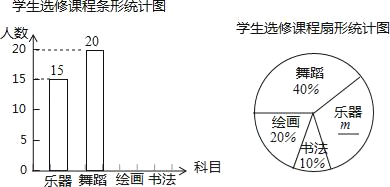
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线![]() ,点D在点C的左边。
,点D在点C的左边。
(1)若BD平分∠ABC,![]() ,则
,则![]() _____°;
_____°;
(2)如图②,若![]() ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明![]() ;
;
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中![]() 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
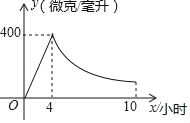
【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某理发店一周的营业额如下表(单位:元):
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
540 | 680 | 760 | 640 | 960 | 2200 | 1780 | 7560 |
(1)求该店本周的日平均营业额.
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上,A点对应的有理数是﹣2,线段AB=12,点P从点A出发,沿AB以每秒1个单位长度的速度向终点B匀速运动;同时点Q从点B出发,沿BA以每秒2个单位长度的速度向终点A匀速运动,设运动时间为ts
(1)请在数轴上标出原点O和B点所对应的有理数:
(2)直接写出PA= ,BQ= (用含t的代数式表示);
(3)当P,Q两点相遇时,求t的值;
(4)当P,Q两点相距5个单位长度时,直接写出线段PQ的中点对应的有理数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
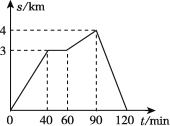
【题目】某人沿一条直路行走,此人离出发地的距离s(km)与行走时间t(min)的关系如图所示,请根据图中提供的信息回答下列问题:
(1)此人在这次行走过程中,停留的时间为 ;
(2)求此人在0~40min这段时间内行走的速度是多少千米/时;
(3)此人在这次行走过程中共走了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
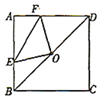
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com