
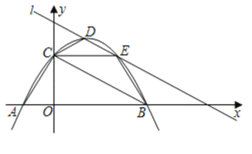
����Ŀ����ƽ��ֱ������ϵ�У���֪������y����![]() x2+bx+c��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C��
x2+bx+c��x�ύ��A(��1��0)��B(3��0)���㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2����ֱ��l����y����![]() x+m��������߽���D��E���㣬��ͼ��
x+m��������߽���D��E���㣬��ͼ��
������CD��CE��BE����S��BCE��3S��CDEʱ����m��ֵ��
���Ƿ����m��ֵ��ʹ��ԭ��O����ֱ��l�ĶԳƵ�P�պ����ڸ��������ϣ�������ڣ���ֱ��д��m��ֵ����������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+
x+![]() ����2����
����2����![]() ���ڴ��ڣ�
���ڴ��ڣ�![]()
��������
��1����A����1��0����B��3��0���������y����![]() x2+bx+cת��Ϊ�ⷽ���鼴�ɽ�����⣮
x2+bx+cת��Ϊ�ⷽ���鼴�ɽ�����⣮
��2��������֤��l��BC����S��BCE��3S��CDE���Ƴ�BC��3DE���Ƴ�ֱ��lӦ����BC���Ϸ�����BC��ȡһ��F��ʹ��BC��3BF���Ƴ��ı���BEDF��ƽ���ı��Σ���C��0��![]() ����B��3��0����BC��3BF���Ƴ�F��2��
����B��3��0����BC��3BF���Ƴ�F��2��![]() ������D��n��
������D��n��![]() n+m������E[n+1��
n+m������E[n+1��![]() ��n+1��+m]�������Ǵ��������ߵĽ���ʽ���ⷽ���鼴�ɽ�����⣮
��n+1��+m]�������Ǵ��������ߵĽ���ʽ���ⷽ���鼴�ɽ�����⣮
����ͼ2�У�����O��OM��BC����������M��M����������ֱ��l����OM��OM�����е㣬���������������M��M�������꼴�ɽ�����⣮
�⣺��1����A����1��0����B��3��0���������y����![]() x2+bx+c�ɵã�
x2+bx+c�ɵã�
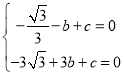 ��
��
��ã�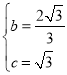 ��
��
�������ߵĽ���ʽΪy����![]() x2+
x2+![]() x+
x+![]() ��
��
��2������ͼ��
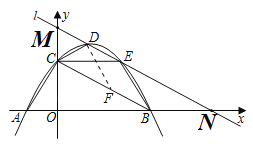
����y����![]() x2+
x2+![]() x+
x+![]() ����x��0���ɵ�y��
����x��0���ɵ�y��![]() ��
��
��C��0��![]() ����
����
��B��3��0����
��OC��![]() ��OB��3��
��OB��3��
��tan��CBO��![]() ��
��
���CBO��30����
��ֱ��l��y����![]() x+m��x�ύ��N��
x+m��x�ύ��N��![]() m��0����y�ύ��M��0��m����
m��0����y�ύ��M��0��m����
��tan��MNO��![]() ��
��![]() ��
��
���NMO��30������CBO��
��l��BC��
��S��BCE��3S��CDE��
��BC��3DE��
��ֱ��lӦ����BC���Ϸ���
��BC��ȡһ��F��ʹ��BC��3BF��
��BF��DE��
���ı���BEDF��ƽ���ı��Σ�
��C��0��![]() ����B��3��0����BC��3BF��
����B��3��0����BC��3BF��
��F��2��![]() ����
����
��D��n��![]() n+m������E[n+1����
n+m������E[n+1����![]() ��n+1��+m]�������Ǵ��������ߵĽ���ʽ�õ���
��n+1��+m]�������Ǵ��������ߵĽ���ʽ�õ���
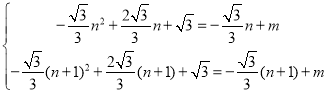 ��
��
��ã� ��
��
��m��ֵΪ![]() ��
��
����ͼ2�У�����O��OM��BC����������M��M����
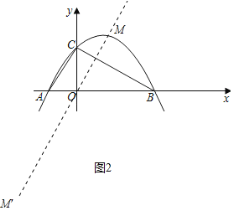
��ֱ��OM�Ľ���ʽΪy��![]() x��
x��
��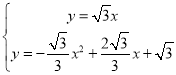 ��
��
��ã�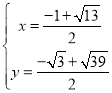 ��
�� ��
��
��M��![]() ��
��![]() ����M����
����M����![]() ��
��![]() ����
����
������ֱ��l����OM��OM�����е㣬
��![]() ��
��![]() ��
��
��ã�m��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
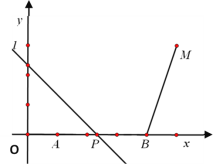
����Ŀ����ͼ����A(1�� 0)��B(4��0)��M(5��3)������P��A���������x����ÿ��1����λ���ٶ������ƶ�������P��ֱ��l��y= -x+bҲ��֮�ƶ������ƶ�ʱ��Ϊt�룮
��1����t=1ʱ����ֱ��l�Ľ���ʽ��
��2����ֱ��l���߶�BM�й����㣬��t��ȡֵ��Χ��
��3������M����ֱ��l�ĶԳƵ�������������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״��С��ȫ��ͬ��С�����ο�Ƭ(��ͼ��)���ص��ķ���һ������Ϊ������(��Ϊm����Ϊn)�ĺ��ӵײ�(��ͼ��)�����ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ���ֵ��ܳ����ǣ� ��
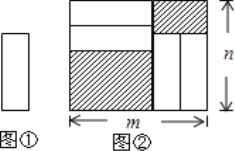
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������һ�������һ�����ߵ�ˮ����һ�Σ�ˮ������Ա��һ����![]() �ı��һ�˷���ˮ���ײ���
�ı��һ�˷���ˮ���ײ���![]() �㣬��һ��¶��ˮ�沢����ˮ����Ե��
�㣬��һ��¶��ˮ�沢����ˮ����Ե��![]() �㣬���ֱ����
�㣬���ֱ����![]() ��û��ˮ�У�¶��ˮ�沿�ֵı����ˮ���
��û��ˮ�У�¶��ˮ�沿�ֵı����ˮ���![]() �ļнǣ�����������ߵĺ������ͬһƽ���ڣ���
�ļнǣ�����������ߵĺ������ͬһƽ���ڣ���

��1����ˮ������ֱ��Ϊ![]() �ᣬ������ͼ��ʾ��ֱ������ϵ�����ˮ������������ߵĽ���ʽ������������ţ���
�ᣬ������ͼ��ʾ��ֱ������ϵ�����ˮ������������ߵĽ���ʽ������������ţ���
��2���ڣ�1���������£���ˮ��������![]() ʱ��ˮ���ԼΪ���٣���
ʱ��ˮ���ԼΪ���٣���![]() ȡ
ȡ![]() �������ȷ��
�������ȷ��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
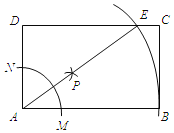
����Ŀ����ͼ������ABCD�У�AD��2����AΪԲ�ģ����ⳤΪ�뾶�������ֱ�AB��AD��M��N���㣬�ֱ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�����������ཻ�ڵ�P������AP���ӳ���CD�ڵ�E����AΪԲ�ģ�AEΪ�뾶�������˻��պù���B����CE�ij�Ϊ_____��
MN�ij�Ϊ�뾶�����������ཻ�ڵ�P������AP���ӳ���CD�ڵ�E����AΪԲ�ģ�AEΪ�뾶�������˻��պù���B����CE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
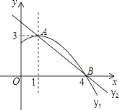
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ� ��2a+b=0����abc��0���۷���ax2+bx+c=3��������ȵ�ʵ����������������x�����һ�������ǣ���1��0�����ݵ�1��x��4ʱ����y2��y1 ��
������ȷ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
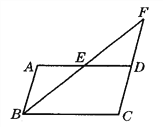
����Ŀ����ͼ��ƽ���ı���ABCD�У���E��AD���е㣬BE���ӳ�����CD���ӳ��߽��ڵ�F��
��1����֤����ABE�ա�DFE��
��2��������BD��AF���ж��ı���ABDF����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
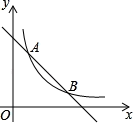
����Ŀ����֪����������y=![]() ��һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��2��6�����͵�B��4��m����
��һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��2��6�����͵�B��4��m����
��1������������һ�κ����Ľ���ʽ��
��2��ֱ��д������ʽ![]() ��ax+b�Ľ⼯�͡�AOB�������
��ax+b�Ľ⼯�͡�AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�������C=900����B=��E=300.



��1������������ͼ2���̶���ABC��ʹ��DEC�Ƶ�C��ת������Dǡ������BC����ʱ����գ��߶�DE��AC��λ�ù�ϵ�� ��
�� ����BDC�����ΪS1����AEC�����ΪS2����S1��S2��������ϵ�� ��
��2��������֤
����DEC�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����S1��S2��������ϵ��Ȼ�����������Էֱ���������BDC����AEC��BC��CE���ϵĸߣ�����֤��С���IJ��롣
��3����չ̽��
��֪��ABC=600����D�����ƽ������һ�㣬BD=CD=4��OE��AB��BC�ڵ�E����ͼ4������������BA�ϴ��ڵ�F��ʹS��DCF =S��BDC,��ֱ��д����Ӧ��BF�ij�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com