
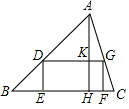
 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | $\sqrt{2}$:3 |
分析 根据题意可以求得AK与KH的比值,从而可以求得AK与AH的比值,然后根据三角形形似即可解答本题.
解答 解:∵矩形DEFG面积与△ADG的面积相等,
∴$\frac{\frac{AK•DG}{2}}{KH•DG}=\frac{1}{1}$,
∴$\frac{AK}{KH}=\frac{2}{1}$,
∴$\frac{AK}{AH}=\frac{2}{3}$,
∵四边形DEFG是矩形,
∴DG∥BC,
∴△ADG∽△ABC,
∴$\frac{DG}{BC}=\frac{AK}{AH}=\frac{2}{3}$,
故选C.
点评 本题考查相似三角形的判定与性质、矩形的性质,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
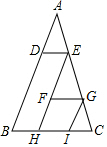 如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.
如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
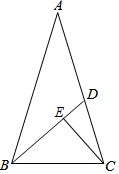 如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )
如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}+3}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com