
【题目】某校开展课外活动,分音乐、体育、美术、制作四个活动项目,随机抽取部分学生对其选择参加的活动项目进行调查统计,制成了两幅不完整的统计图.
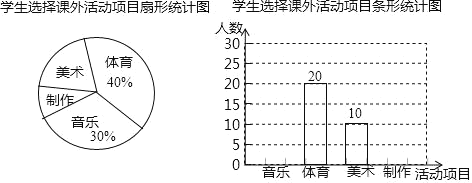
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 ;
(2)请补全上述条形统计图,并求出扇形图中“美术”所占的圆心角度数;
(3)若该校有2000名学生,请你用此样本估计参加“艺术”类活动项目(“艺术”类活动包括“音乐”和“美术”两个项目)的学生人数约为多少人.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧![]() 的长为
的长为![]() ,直线
,直线![]() 与x轴、y轴分别交于点A、B.
与x轴、y轴分别交于点A、B.
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
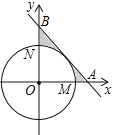
查看答案和解析>>
科目:初中数学 来源: 题型:
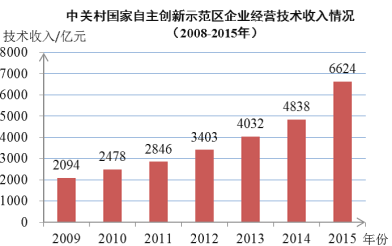
【题目】上图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.
下面四个推断:
①2009 年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是3403亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入平均增长率比2013年到2015年技术收入平均增长率大.
其中,正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
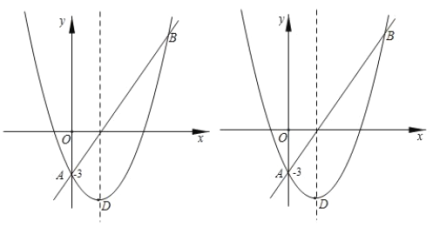
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某渔场计划购买甲、乙两种鱼苗共6000尾,甲种鱼苗每尾0.5元,乙种鱼苗每尾0.8元.相关资料表明:甲、乙两种鱼苗的成活率分别为90%和95%.
(1)若购买这批鱼苗共用了3600元,求甲、乙两种鱼苗各购买了多少尾?
(2)若购买这批鱼苗的钱不超过4200元,应如何选购鱼苗?
(3)若要使这批鱼苗的成活率不低于93%,且购买鱼苗的总费用最低,应如何选购鱼苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
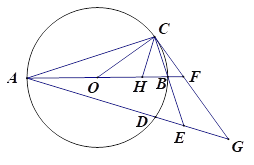
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
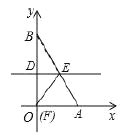
【题目】将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]()
(I)过边![]() 上的动点
上的动点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于点
于点![]() ,沿着
,沿着![]() 折叠该纸片,点
折叠该纸片,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处.
处.
①如图,当![]() 为
为![]() 中点时,求
中点时,求![]() 点的坐标;
点的坐标;
②连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 点坐标:
点坐标:
(Ⅱ)![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线折叠,得到
所在的直线折叠,得到![]() ,连接
,连接![]() ,当
,当![]() 取得最小值时,求
取得最小值时,求![]() 点坐标(直接写出结果即可).
点坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列结论:
①二次函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
②关于![]() 的方程
的方程![]() 的解是
的解是![]() ,
,![]() (
(![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() ),则方程
),则方程![]() 的解是
的解是![]() ,
,![]() .
.
③设二次函数![]() ,当
,当![]() 时,总有
时,总有![]() ,当
,当![]() 时,总有
时,总有![]() ,那么
,那么![]() 的取值范围是
的取值范围是![]() .
.
其中,正确结论的个数是( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
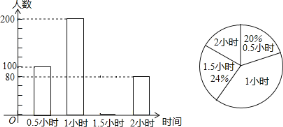
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com