Question

【题目】平面直角坐标系中，点、分别在函数与的图象上， 、的横坐标分别为、。

(1)若轴，求的面积；

(2)若是以为底边的等腰三角形，且a，求的值；

(3)作边长为2的正方形，使轴，点在点的左上方，那么，对大于或等于的任意实数， 边与函数的图象都有交点，请说明理由。

Answer 1

【答案】(1) 的面积为3；

(2) 的值为-3;

(3)理由见解析.

【解析】试题分析：（1）根据反比例函数系数k的几何意义得出△OAC与△OBC的面积，再求和即可；

（2）分别用a、b表示出A、B两点的坐标，再根据勾股定理得出OA2=a2+（）2，OB2=b2+（-）2，由OA=OB即可得出结论；

（3）根据题意画出图形，设直线CD与函数y=（x＞0）的图象交点为F，用a表示出A、C两点的坐标，进而可得出F点的坐标，求出FC的最大值，进而可得出结论．

试题解析：（1）如图1，AB交y轴于C，

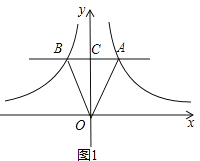
∵AB∥x轴，

∴S△OAC=×|3|=，S△OBC=×|-3|=，

∴S△OAB=S△OAC+S△OBC=3；

（2）∵点A、B分别在函数y=（x＞0）与y=-（x＜0）的图象上，A、B的横坐标分别为a、b．

∴A（a， ）、B（b， ），

∴OA2=a2+（）2，OB2=b2+（-）2，

当OA=OB时，OA2=OB2

∴a2+（）2=b2+（-）2，

整理得：a2b2（a2-b2）=9（a2-b2）．

∵a+b≠0，a＞0，b＜0，

∴a2-b2≠0

∴a2b2=9，

∴ab=-3；

（3）设直线CD与函数y=（x＞0）的图象交点为F，如图2，

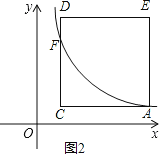
∵A点坐标为（a， ），正方形ACDE的边长为3，

∴C点坐标为（a-3， ），

∴F点的坐标为（a-3， ），

∴FC=-=．

∵a（a-3）=（a-）2-，当a＞时，a（a-3）的值随a的值的增大而增大，

∴a（a-3）的最小值为3，

∴FC的最大值为3，即FC≤DC，

∴CD与函数y=（x＞0）的图象有交点．

特别地，当a=3时，点A的坐标为（3，1），此时C（1，1）、D（1，3），

此时点D落在函数y=（x＞0）的图象上．

∴点F在线段DC上，即对大于或等于3的任意实数a，CD边与函数y=（x＞0）的图象都有交点．