
【题目】(本题4分+5分=9分)
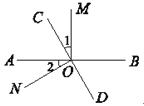
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOC的度数;(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
【答案】(1)90°;(2)150°
【解析】试题分析:(1)由垂线的性质求得∠AOM=∠BOM=90°,然后根据等量代换及补角的定义解答;
(2)根据垂线的定义求得∠AOM=∠BOM=90°,再由∠1=![]() ∠BOC求得∠BOC=120°;然后根据对顶角的性质及补角的定义解答即可.
∠BOC求得∠BOC=120°;然后根据对顶角的性质及补角的定义解答即可.
试题解析:(1)∵OM⊥AB,∠1=∠2,
∴∠1+∠AOC=∠2+∠AOC=90°,即∠CON=90°;
又∠NOC+∠NOD=180°,
∴∠NOD=90°;
(2)∵OM⊥AB,∠1=![]() ∠BOC,
∠BOC,
∴∠BOC=120°,∠1=30°;
又∠AOC+∠BOC=180°,
∴∠AOC=60°;
而∠AOC=∠BOD(对顶角相等),
∴∠MOD=∠MOB+∠AOC=150°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
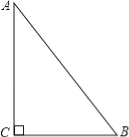
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为12?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
![]()
水银柱的长度x(cm) | 4.2 | … | 8.2 | 9.8 |
体温计的读数y(℃) | 35.0 | … | 40.0 | 42.0 |
(1)求y关于x的函数关系式(不需要写出函数的定义域);
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
(1)任何一个有理数的平方都是正数; (2)两个数比较,绝对值大的反而小;
(3)- a不一定是负数 (4)符号相反的两个数互为相反数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程。
(1)解题与归纳
①小明摘选了以下各题,请你帮他完成填空。
![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
②归纳:对于任意数a,有![]() =
=
③小芳摘选了以下各题,请你帮她完成填空。
![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
④归纳:对于任意非负数a,有![]() =
=
(2)应用
根据他们归纳得出的结论,解答问题。
数a,b在数轴上的位置如图所示,化简: ![]() -
-![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
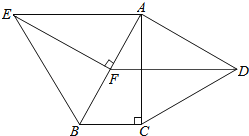
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com