
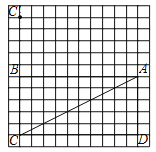
【题目】如图,12×12的正方形网格中的每个小正方形的边长都是1,正方形的顶点叫做格点.矩形ABCD的四个顶点A,B,C,D都在格点上,将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点.
(1)在正方形网格中确定D′的位置,并画出△AD′C′;
(2)若边AB交边C′D′于点E,求AE的长.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
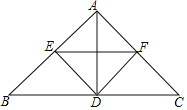
【题目】如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是

A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
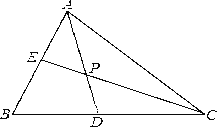
【题目】如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五·一车展”期间,某汽车经销商推出![]() 四种型号的轿车共1000辆进行展销,
四种型号的轿车共1000辆进行展销,![]() 型号轿车销售的成交率(售出数量
型号轿车销售的成交率(售出数量![]() 展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)
展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)

(1)参加展销的![]() 型号轿车有多少辆?
型号轿车有多少辆?
(2)请你将图2的统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移
分别向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位,分别得到点
个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .(三角形可用符号
.(三角形可用符号![]() 表示,面积用符号
表示,面积用符号![]() 表示)
表示)

(1)直接写出点![]() ,
,![]() 的坐标.
的坐标.
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() ,
,![]() .
.
①若![]() 在线段
在线段![]() 之间时(不与
之间时(不与![]() ,
,![]() 重合),求
重合),求![]() 的取值范围;
的取值范围;
②若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
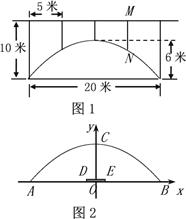
【题目】一座拱桥的截面轮廓为抛物线型(如图1),拱高6米,跨度20米,相邻两支柱间的距离均为5米.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是![]() 的形式. 请根据所给的数据求出
的形式. 请根据所给的数据求出![]() 的值.
的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间DE是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2米、高3米的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com