
 ʱ����AB��B���BEF�Ƿ����ƣ������ƣ������֤�����������ƣ���Ҫ˵�����ɣ�
ʱ����AB��B���BEF�Ƿ����ƣ������ƣ������֤�����������ƣ���Ҫ˵�����ɣ�
 BC����������Rt��ABG�У��ɹ��ɶ������AE�ij���
BC����������Rt��ABG�У��ɹ��ɶ������AE�ij��� ʱ��x+y=
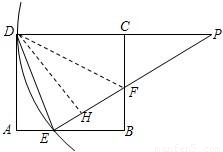
ʱ��x+y= ��������2���ĺ�����ϵʽ����ô�ʱx��ֵ�����������AE��BF�ij��������۵�������֪��EF��ֱƽ��BB�䣬�费��ΪQ����Rt��BEF�У�����ֱ������������IJ�ͬ��ʾ�����������BQ�ij���Ҳ�͵ó���BB��ij���Ȼ�����ж�����ֱ�������εĶ�Ӧ���Ƿ�ɱ������ɣ�
��������2���ĺ�����ϵʽ����ô�ʱx��ֵ�����������AE��BF�ij��������۵�������֪��EF��ֱƽ��BB�䣬�费��ΪQ����Rt��BEF�У�����ֱ������������IJ�ͬ��ʾ�����������BQ�ij���Ҳ�͵ó���BB��ij���Ȼ�����ж�����ֱ�������εĶ�Ӧ���Ƿ�ɱ������ɣ�
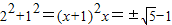 ��������ȥ������1�֣�
��������ȥ������1�֣�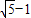 ��
��
 ����2�֣�
����2�֣�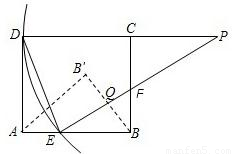
 ��
��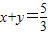 ��
�� ��
��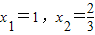 ����1�֣�
����1�֣� ��
�� ��BB'=
��BB'= ��
��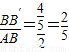 ��
��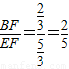 ��
��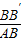 =
=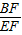 ��
��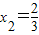 ʱ��
ʱ�� ��
��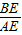 =
= =2��
=2�� =1��
=1�� ��AE=1ʱ����AB'B�ס�BEF��
��AE=1ʱ����AB'B�ס�BEF�� ��
��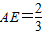 ʱ����AB'B���BEF�����ƣ�
ʱ����AB'B���BEF�����ƣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2010���Ϻ��з������п���ѧһģ�Ծ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
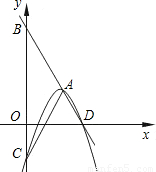
��Ŀ��������ѧ ��Դ��2010���Ϻ��з������п���ѧһģ�Ծ��������棩 ���ͣ�ѡ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010���Ϻ��з������п���ѧһģ�Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010���Ϻ��з������п���ѧһģ�Ծ��������棩 ���ͣ������
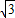 ����ô�½Ǧ�= �ȣ�
����ô�½Ǧ�= �ȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com