
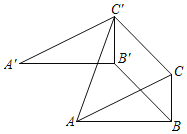
【题目】定义:有一组邻边相等的凸四边形叫做等邻边四边形.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB'的方向平移,得到A'B'C',连接AC',CC',若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是_____.
【答案】1或![]() .
.
【解析】
由平移的性质得到![]() ,① 当
,① 当![]() 时,
时,![]() ;② 如图1,当
;② 如图1,当![]() 时,③如图2,当
时,③如图2,当![]() 时,则
时,则![]() ,延长
,延长![]() 交AB于H,设
交AB于H,设![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
解:∵将Rt△ABC平移得到![]() ,
,
![]() ,
,
① 当![]() 时,
时,![]() ;
;
②如图1,当![]() 时,
时,
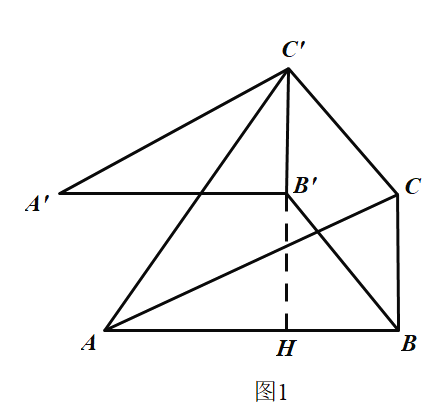
∵∠ABC=90°,![]() 是∠ABC的角平分线,
是∠ABC的角平分线,
∴![]() ,
,
延长![]() 交AB于H,
交AB于H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
![]()
∴22=(2﹣x)2+(1+x)2,
整理方程为:2x2﹣2x+1=0,
∵△=4﹣8=﹣4<0,
∴此方程无实数根,故这种情况不存在;
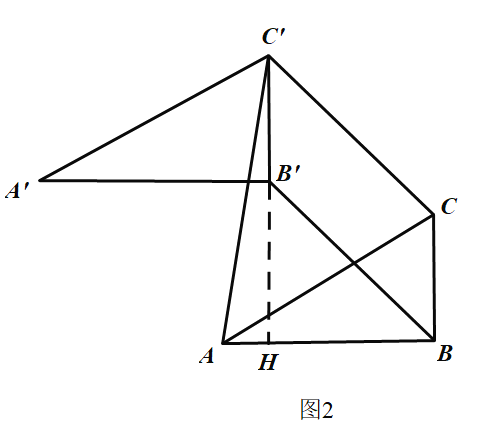
③如图2,当当![]() 时,则
时,则![]() ,
,
延长![]() 交AB于H,
交AB于H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
![]()
∴(![]() x)2=(2﹣x)2+(1+x)2,
x)2=(2﹣x)2+(1+x)2,
解得:x=![]() ,
,
∴BB′=![]() ,
,
综上所述,若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是1或![]() ,
,
故答案为:1或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
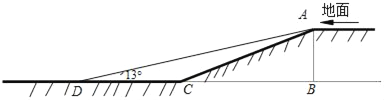
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
(1)求半径OB的长;
(2)如果点P是弧AB的中点,联结PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP、CA交于点D,求线段DP的长.
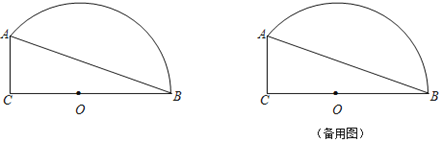
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() .当起重臂
.当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为118°.
为118°.
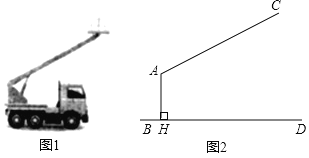
(1)求操作平台![]() 离地面的高度;
离地面的高度;
(2)当张角![]() 为120°,其它条件不变时,求操作平台
为120°,其它条件不变时,求操作平台![]() 升高的高度.
升高的高度.
(最后结果精确到0.1,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线OE的对称点,是否存在点
关于直线OE的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 上?若存在,请直接写出相应的点
上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com