【题目】在平面直角坐标系中，对于平面内任一点P （a，b）若规定以下两种变换：①f（a，b）=（﹣a，﹣b），如f（1，2）=（﹣1，﹣2）；②g（a，b）=（b，a），如g（1，3）=（3，1）按照以上变换，那么f（g（a，b））等于（ ）
A. （﹣b，﹣a） B. （a，b） C. （b，a） D. （﹣a，﹣b）
科目：初中数学 来源： 题型：
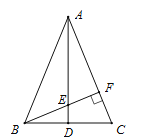
【题目】如图，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上，BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC＝45°
求证：△AEF≌△BCF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x，y的方程组
. 给出下列结论：
①
是方程组的解；②当k＝
时，x ，y的值互为相反数；
③若方程组的解也是方程x + y ＝4 – k的解，则k＝1；
④若
，则
. 其中正确的是________。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，BE=DF．
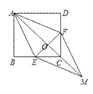
（1）求证：AE=AF；
（2）连接AC交EF于点O，延长OC至点M，使OM=OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
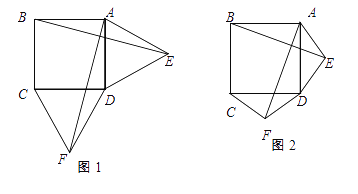
【题目】如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE.
（Ⅰ）请写出AF与BE的数量关系与位置关系分别是什么，并证明.
（Ⅱ）如图2，若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF，且EA=ED=FD=FC，第（1）问中的结论是否仍然成立?请作出判断并给予证明；
查看答案和解析>>
科目：初中数学 来源： 题型：
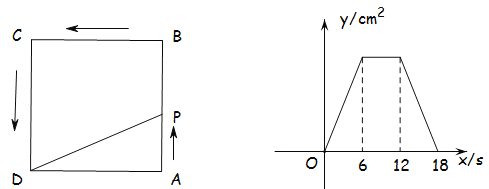
【题目】如图①,在正方形
中，点
以
的速度从点
出发按箭头方向运动，到达点
停止. 
的面积
与运动时间
之间的函数图像如图②所示.(规定:点
在点
， 
时， 
）
发现:(1) 
= _______ 
，当
时， 
=_________ 
；
(2)当点
在线段_________上运动时， 
的值保持不变.
拓展:求当
及
时， 
与
之间的函数关系式.
探究:当
为多少时， 
的值为
？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
