
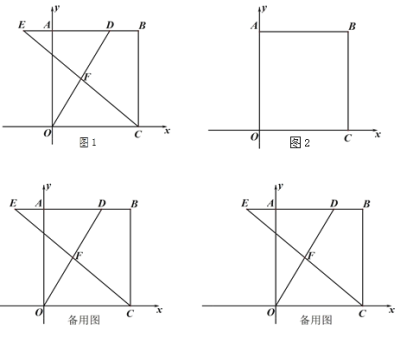
【题目】矩形OABC的顶点O与坐标原点重合,点B的坐标为(6,8),动点D、E分别从点B、A同时出发,沿射线BA运动,点D、E的运动速度均为每秒2个单位,设D、E的运动时间为t秒.连接OD、CE交于点F.
(1)如图1,求点F的纵坐标;
(2)若点G为OA的中点,在点D、E运动过程中,设△GEF的面积为y,求y与t的关系式;
(3)在(2)的条件下,连接BG,线段BG、OD交于点K,若![]() ,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
【答案】(1)4 (2)![]() (3)存在,点M的坐标为
(3)存在,点M的坐标为![]()
【解析】
(1)根据矩形的性质可证明![]() ,即可得
,即可得![]() ,从而求出点F的纵坐标;
,从而求出点F的纵坐标;
(2)如图,连接EG、FG,根据三角形面积公式求解即可;
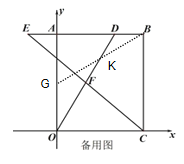
(3)连接BG,线段BG、OD交于点K,根据![]() ,求出t的值,即可得到点E、点D的坐标,再联立直线GB和直线OD的解析式求出K的坐标,根据平行四边形对角线互相平分求解出M的坐标即可.
,求出t的值,即可得到点E、点D的坐标,再联立直线GB和直线OD的解析式求出K的坐标,根据平行四边形对角线互相平分求解出M的坐标即可.
(1)∵动点D、E分别从点B、A同时出发,沿射线BA运动,点D、E的运动速度均为每秒2个单位
∴![]()
∵四边形OABC是矩形
∴![]()
∴![]()
在△EDF和△COF中
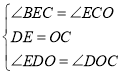
∴![]()
∴![]()
∴点F的纵坐标为![]() ;
;
(2)如图,连接EG、FG
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵G是OA的中点
∴![]()
∴![]()
∴![]()
∴![]() ;
;
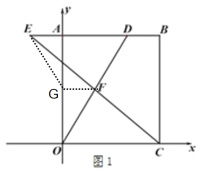
(3)存在,连接BG,线段BG、OD交于点K,
∵![]() ,
,![]()
∵![]()
∴![]()
∴![]() ,
,![]()
解得![]()
∵连接BG,线段BG、OD交于点K
∴![]()
∴![]()
∴![]()
设直线GB的解析式为![]()
将![]() 代入
代入![]() 中
中
![]()
解得![]()
∴![]()
设直线OD的解析式为![]()
将![]() 代入
代入![]() 中
中
![]()
解得![]()
![]()
联立方程得
![]()
解得![]()
将![]() 代入
代入![]() 中
中
![]()
∴![]()
∴![]()
设![]()
①对角线为KE时
![]()
解得![]()
∴![]()
②对角线为DE时
![]()
解得![]()
∴![]()
③对角线为KD时
![]()
解得![]()
∴![]()
故存在,点M的坐标为![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
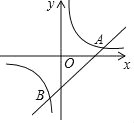
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)分别交于点A(4,1),B(﹣1,a)
(m≠0)分别交于点A(4,1),B(﹣1,a)
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出kx+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( )
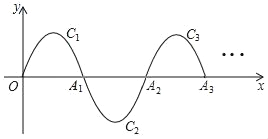
A. 4 B. ﹣4 C. ﹣6 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
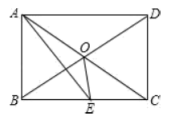
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形OABC的顶点O在坐标原点,顶点A,C在反比例函数y=![]() 的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.
的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
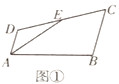
【题目】在数学活动课上,数学老师出示了如下题目:
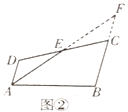
如图①,在四边形![]() 中,
中,![]() 是边
是边![]() 的中点,
的中点,![]() 是
是![]() 的平分线,
的平分线,![]() .
.
求证:![]() .
.
小聪同学发现以下两种方法:
方法1:如图②,延长![]() 、
、![]() 交于点
交于点![]() .
.
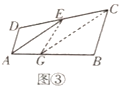
方法2:如图③,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() .
.
(1)请你任选一种方法写出这道题的完整的证明过程;
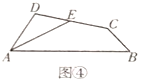
(2)如图④,在四边形![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
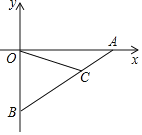
【题目】在平面直角坐标系中点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点且
轴上的点且![]() 点的坐标是
点的坐标是![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,是靠近点
上,是靠近点![]() 的三等分点.点
的三等分点.点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)试确定该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
(2)试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com