���Ķ����ģ��ٻش���ĺ�������⣮
ƽ������һ������F��һ����ֱ��l�ľ�����ȵĵ�Ĺ켣���������ߣ���F���������ߵĽ��㣬ֱ��l���������ߵ��ߣ�
������������ߵĶ��壬�������������ߵķ��̣�
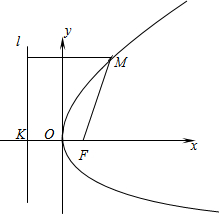
����ͼ������ֱ������ϵxoy��ʹx�ᾭ����F�Ҵ�ֱ��ֱ��l������ΪK����ʹԭ�����߶�KF���е��غϣ���|KF|=p��p��0������ô����F������Ϊ��
��0������l�ķ���Ϊx=-
��
���M��x��y����������������һ�㣬��M��l�ľ���Ϊd���������ߵĶ��壬�����߾�������|MF|=d�ĵ�M�Ĺ켣��
��|MF|=
��d=|x+
|��
=|x+
|
����ʽ����ƽ��������y
2=2px��p��0����
���̢ٽ��������ߵı����̣�����ʾ�������ߵĽ�����x����������ϣ������ǣ�
��0���������߷�����x=-
��
һ�������ߣ�������������ƽ���ڵ�λ�ò�ͬ������Ҳ��ͬ�����������ߵı����̻��������ļ�����ʽ��y
2=-2px��x
2=2py��x
2=-2py�������������ߵı����̣����������Լ��߷����б����£�
| ������ |
�������� |
�߷��� |
| y2=2px��p��0�� |
����0�� |
x=- |
| y2=-2px��p��0�� |
��-��0�� |
x= |
| x2=2py��p��0�� |
��0���� |
y=- |
| x2=-2py��p��0�� |
��0��-�� |
y=- |
����������⣺
��1������֪�����ߵı�������y
2=8x�������Ľ���������
���߷�����
����֪�����ߵĽ���������F��0��-6���������ı�������
��
��2����M���F��4��0���ľ��������ֱ��l��x+5=0�ľ���С1�����M�Ĺ켣���̣�
��3��ֱ��
y=x+b����������y
2=4x�Ľ��㣬���������ཻ������A��B�����߶�AB�ij���


 �Ʊȣ�a��b����
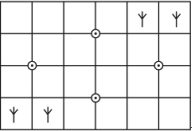
�Ʊȣ�a��b���� �����ƣ����д�С���ֲ�ͬ�ļ�Ǯ������ͼ��ʾ���㳤10����ÿ��10Ԫ���㳤13����ÿ��15Ԫ�����Ӳ�֪�������ָ���Щ�����ܷ�����������⣮
�����ƣ����д�С���ֲ�ͬ�ļ�Ǯ������ͼ��ʾ���㳤10����ÿ��10Ԫ���㳤13����ÿ��15Ԫ�����Ӳ�֪�������ָ���Щ�����ܷ�����������⣮ ���Ķ����ģ��ٻش���ĺ�������⣮
���Ķ����ģ��ٻش���ĺ�������⣮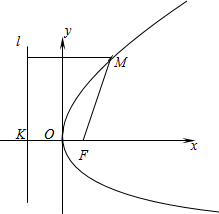 ���Ķ����ģ��ٻش���ĺ�������⣮
���Ķ����ģ��ٻش���ĺ�������⣮ ��0������l�ķ���Ϊx=-
��0������l�ķ���Ϊx=- ��
��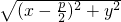 ��d=|x+
��d=|x+ |��
|��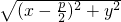 =|x+
=|x+ |
| ��0���������߷�����x=-
��0���������߷�����x=- ��
��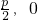 ��
��
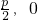 ��
��
 ��
��
 ��
��
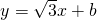 ����������y2=4x�Ľ��㣬���������ཻ������A��B�����߶�AB�ij���
����������y2=4x�Ľ��㣬���������ཻ������A��B�����߶�AB�ij��� �Ʊȣ�a��b����
�Ʊȣ�a��b���� ������V����V���ֱ��ʾ��������������������
������V����V���ֱ��ʾ��������������������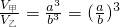 ��
�� �����ƣ����д�С���ֲ�ͬ�ļ�Ǯ������ͼ��ʾ���㳤10����ÿ��10Ԫ���㳤13����ÿ��15Ԫ�����Ӳ�֪�������ָ���Щ�����ܷ�����������⣮
�����ƣ����д�С���ֲ�ͬ�ļ�Ǯ������ͼ��ʾ���㳤10����ÿ��10Ԫ���㳤13����ÿ��15Ԫ�����Ӳ�֪�������ָ���Щ�����ܷ�����������⣮ ������V����V���ֱ��ʾ��������������������
������V����V���ֱ��ʾ�������������������� ��
��
