
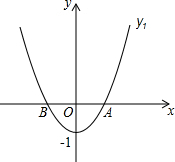
 ��ͼ����ƽ��ֱ������ϵ�У�������y1=x2-1��x�ύ�ڵ�A�͵�B����A�ڵ�B���Ҳࣩ��������y2�Ľ���ʽΪy2=$\frac{1}{1-n}$��x-n��2+n-1��n��1��ֱ��y3�Ľ���ʽΪy3=x-2��
��ͼ����ƽ��ֱ������ϵ�У�������y1=x2-1��x�ύ�ڵ�A�͵�B����A�ڵ�B���Ҳࣩ��������y2�Ľ���ʽΪy2=$\frac{1}{1-n}$��x-n��2+n-1��n��1��ֱ��y3�Ľ���ʽΪy3=x-2������ ��1�������Ա����뺯��ֵ�Ĺ�ϵ���ɵ�A�����꣬�����Ա�����ֵ���ɵ�y2��y3��ֵ��
��2��������ͬ�ĺ���ֵ��Ӧ���Ա������ڶԳ���Գƣ��ɵ�C���������BC�ľ��룬�ɵ�n��ֵ������n��ֵ���ɵ�y2�ĺ�������ʽ��
��3����������Ƚϣ��ɵö�������x����n��0ʱ��y1��y2��y3�Ĵ�С��ϵ��
��� �⣺��1����y1=x-1�У���y1=0ʱ��x2-1=0��
���x1=1��x2=-1��
�ߵ���B����Ҳ࣬
��A��������1��0����
��x=1����y2=$\frac{1}{1-n}$��x-n��+n-1��3=2x-2��
��y2=0��y3=0��
��������y2��y3����A�㣻
��2����y2=$\frac{1}{1-n}$��x-n��2+n-1��
��Գ���Ϊֱ��x=n��
�ɣ�1��֪������y2=$\frac{1}{1-n}$��x-n��2+n-1����A��1��0����
���C��2n-1��0����
BC=2AB��AB=2��
��|2n-1-��-1��|=4��
��� n=2��n=-2��
��ʱy2�Ľ���ʽΪy2=-��x-2��2+1��y2=$\frac{1}{3}$��x+2��2-3��
��3����ͼ�� ��
��
��������x����n��0ʱ������y1��y2��3��
���ɣ�y1-y2=x2-1-$\frac{1}{1-n}$��x-n��2-n+1=$\frac{n��x-1��2}{n-1}$��
�֡ߡ�0��
��y1-y2��0��
��y1��y2��
ͬ��y2-y3=$\frac{1}{1-n}$��x-n��2+n-1-2x+2=$\frac{��x-1��^{2}}{1-n}$��
�֡ߡ�0��
��y2-y3��0��
��y2�ݡ�y3��
��������x����n��0ʱ������y1��y2��3��
���� ���⿼���˶��κ����ۺ��⣬�������Ա����ں���ֵ�Ķ�Ӧ��ϵ����ͬ�ĺ���ֵ�ĵ���ڶԳ���Գƣ������ľ��빫ʽ�ó�n��ֵ����������ȽϺ���ֵ�Ĵ�С��ϵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  ƽ���ı��� | B�� |  Բ | C�� |  ������� | D�� |  ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
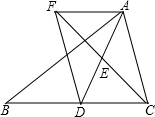 ��֪����ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬����AD��ȡAD���е�E������A��BC��ƽ������CE���ӳ��߽��ڵ�F������DF����֤��AF=DC��
��֪����ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬����AD��ȡAD���е�E������A��BC��ƽ������CE���ӳ��߽��ڵ�F������DF����֤��AF=DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
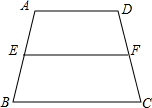 ��ͼ����֪�ı���ABCD�У�AD��BC����E��F�ֱ�Ϊ��AB��CD���е㣬����EF����֪AD=4��BC=6����EF�ij���
��ͼ����֪�ı���ABCD�У�AD��BC����E��F�ֱ�Ϊ��AB��CD���е㣬����EF����֪AD=4��BC=6����EF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
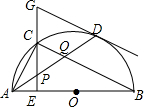 ��ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��$\widehat{AD}$���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD=��ABC����GP=GD���۵�P�ǡ�ACQ�����ģ�������ȷ�����Ǣڢۣ�ֻ����д��ţ���
��ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��$\widehat{AD}$���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD=��ABC����GP=GD���۵�P�ǡ�ACQ�����ģ�������ȷ�����Ǣڢۣ�ֻ����д��ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com