解:(1)平行四边形;
(2)△BEF≌△CDF或(△AFB≌△EBC≌△EFC)
证明:连接DE,
∵AB=2CD,E为AB中点,
∴DC=EB,
又∵DC∥EB,
∴四边形BCDE是平行四边形,
∵AB⊥BC,

∴四边形BCDE为矩形,
∴∠AED=90°,∠CDE=∠BED=90°,BE=CD,
在Rt△AED中,∠A=60°,F为AD的中点,
∴AF=

AD=EF,
∴△AEF为等边三角形,
∴∠DFE=180°-60°=120°,
∵EF=DF,
∴∠FDE=∠FED=30°.
∴∠CDF=∠BEF=120°,
在△BEF和△FDC中,
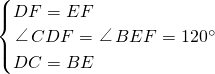
,
∴△BEF≌△CDF(SAS).(其他情况证明略)
(3)若CD=2,则AD=4,
∵∠A=60°,
∴sin60°=

=

,
∴DE=AD•

=2

∴DE=BC=2

,
∵四边形AECD为平行四边形,
∴S
△ECF与S
四边形AECD等底同高,
∴S
△ECF=

S
四边形AECD=

CD•DE=

×2×2

=2

,
S
△CBE=

BE•BC=

×2×2

=2

,
∴S
四边形BCFE=S
△ECF+S
△EBC=2

+2

=4

.
分析:(1)根据题意可知AE∥CD且AE=CD,所以四边形AECD是平行四边形.
(2)连接DE,证出四边形DEBC是矩形,再加上F是AD的中点,∠A=60°,可得出△AFE是等边三角形,那么就可证出△BEF≌△FDC.
(3)因为F是AD的中点,所以能得出△EFC的面积是平行四边AECD的面积的一半,再加上∠A=60°,可求出DE(BC=DE)的长,再利用三角形的面积公式计算就可以了.
点评:本题主要运用了平行四边形的判定和性质,以及矩形的判定和性质,还有全等三角形的判定和性质,三角形的面积公式等内容.

 EC、BF、CF.
EC、BF、CF.
 AD=EF,
AD=EF,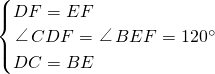 ,
, =
= ,
, =2
=2
 ,
, S四边形AECD=
S四边形AECD= CD•DE=
CD•DE= ×2×2
×2×2 =2
=2 ,
, BE•BC=
BE•BC= ×2×2
×2×2 =2
=2 ,
, +2
+2 =4
=4 .
.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为