
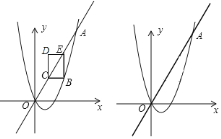
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() .
.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 点
点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,过点
之间的一个动点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() 、
、![]() ,以
,以![]() 、
、![]() 为边构造矩形
为边构造矩形![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求
,求![]() ,
,![]() 之间的关系式.
之间的关系式.
![]() 将射线
将射线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线交于点
后与抛物线交于点![]() ,求
,求![]() 点的坐标.
点的坐标.
【答案】![]()
![]() ;
;![]()
![]() 、
、![]() 之间的关系式为
之间的关系式为![]() ;
;![]()
![]() 点的坐标为
点的坐标为![]() .
.
【解析】
(1)把点A的坐标代入一次函数解析式求得a的值;然后把点A的坐标代入二次函数解析式来求b的值即可;
(2)根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式;
(3)如图2,作∠POA=45°,交抛物线与P,过P作PQ⊥OA于Q,过P作PM⊥x轴于M,过Q作QN⊥PM于N交y轴于R,构建全等三角形△PNQ≌△QRO,结合全等三角形的对应边相等和二次函数图象上点的坐标特征来求点P的坐标.
![]() ∵点
∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
解得:![]() ,
,
又∵点![]() 是抛物线
是抛物线![]() 上的一点,
上的一点,
将点![]() 代入
代入![]() ,可得
,可得![]() ,
,
∴抛物线解析式为![]() ;
;
![]() 如图
如图![]() ,∵直线
,∵直线![]() 的解析式为:
的解析式为:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
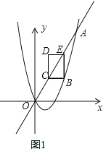
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
把点![]() 代入
代入![]() ,可得
,可得![]() ,
,
∴![]() 、
、![]() 之间的关系式为
之间的关系式为![]() ;
;
![]() 如图
如图![]() ,作
,作![]() ,交抛物线与
,交抛物线与![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 于
于![]() 交
交![]() 轴于
轴于![]() ,
,
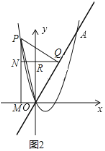
则PQ=OQ,
则![]() ,
,
所以![]() ,
,![]() ,
,
设![]() 点为
点为![]() ,则
,则![]() 为
为![]() ,代入抛物线解析式得
,代入抛物线解析式得![]() ,
,
解得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )
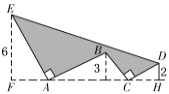
A.50B.44C.38D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
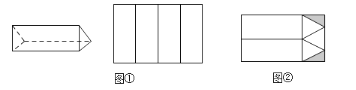
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第一次操作,把抛物线
称为第一次操作,把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第二次操作,…,以此类推,则抛物线
称为第二次操作,…,以此类推,则抛物线![]() 经过第
经过第![]() 此操作后得到的抛物线
此操作后得到的抛物线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()

![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
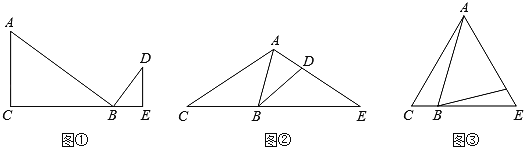
【题目】已知,点B在线段CE上.
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今通过微信朋友圈发布自己每天行走的步数已成为一种时尚.“健身达人”小张为了了解他的微信朋友圈里大家的运动情况,随机抽取了部分好友进行调查,把他们1月29日那天每人行走的步数情况分为五个类别:A(0~4000步)(说明:0~4000表示大于或等于0,小于或等于4000,下同)、B(4001~8000步)、C(8001~12000步)、D(12001~16000步)、E(16000步以上),并将统计结果绘制了如图1和2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)小张随机抽取了 名微信朋友圈好友;
(2)将图1的条形统计图补充完整;
(3)已知小张的微信朋友圈里共300人,请根据本次抽查的结果,估计在它的微信朋友圈里1月29日那天行走不超过8000步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
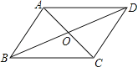
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
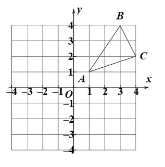
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)在图中画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)通过平移,使![]() 移动到原点
移动到原点![]() 的位置,画出平移后的
的位置,画出平移后的![]() .
.
(3)在![]() 中有一点
中有一点![]() ,则经过以上两次变换后点
,则经过以上两次变换后点![]() 的对应点
的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com