
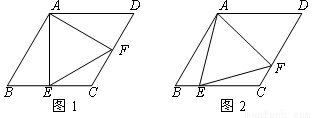
如图,菱形ABCD中,∠B=60º,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60º,
求证:BE=DF;
(2)如图2,若∠EAF=60º,
求证:△AEF是等边三角形.
证明:(1)连接AC。
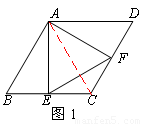
∵菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°-∠B=120°。
∴△ABC是等边三角形。
∵E是BC的中点,∴AE⊥BC。
∵∠AEF=60°,∴∠FEC=90°-∠AEF=30°。
∴∠CFE=180°-∠FEC-∠C=180°-30°-120°=30°。∴∠FEC=∠CFE。
∴EC=CF。∴BE=DF。
(2)连接AC。
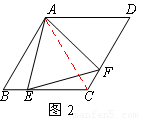
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC,∠D=∠B=60°,∠ACB=∠ACF。
∴△ABC是等边三角形。
∴AB=AC,∠ACB=60°。∴∠B=∠ACF=60°。
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD。
∴∠AEB=∠AFC。
在△ABE和△AFC中,∵∠B=∠ACF,∠AEB=∠AFC, AB=AC,
∴△ABE≌△ACF(AAS)。∴AE=AF。
∵∠EAF=60°,∴△AEF是等边三角形。
【解析】菱形的性质,等边三角形的判定和性质,三角形内角和定理 全等三角形的判定和性质。
【分析】(1)连接AC,由菱形ABCD中,∠B=60°,根据菱形的性质,易得△ABC是等边三角形,
又由三线合一,可证得AE⊥BC,从而求得∠FEC=∠CFE,即可得EC=CF,从而证得BE=DF。
(2)连接AC,可得△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得:△AEF是等边三角形。


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
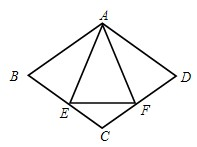 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )A、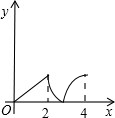 | B、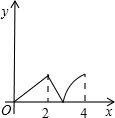 | C、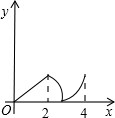 | D、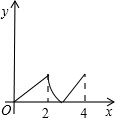 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com