
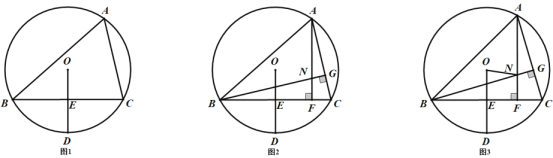
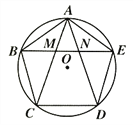
【题目】![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,交
,交![]() 边于点
边于点![]() ,且
,且![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)60° (2)见解析 (3)![]()
【解析】
(1)利用等腰三角形的性质结合圆周角定理得出答案;
(2)过![]() 做
做![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,利用AAS得出
,利用AAS得出![]() ,进而得出答案;
,进而得出答案;
(3)首先证明四边形![]() 是菱形,可证
是菱形,可证![]() (SAS),则可得
(SAS),则可得![]() 是等边三角形, 设
是等边三角形, 设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]() ,根据四边形
,根据四边形![]() 内接于
内接于![]() ,则有:
,则有:![]() ,可得
,可得![]() (SAS),设
(SAS),设![]() ,则
,则![]() ,利用勾股定理得
,利用勾股定理得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,再根据
,再根据![]() ,得
,得![]()
解得![]() ,进而得出答案.
,进而得出答案.
(1)如图示,连接![]() ,
,

![]() ,
,![]() ,
,![]()
![]() ,
,
![]() .
.
(2)如图示,连接![]() ,过
,过![]() 做
做![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
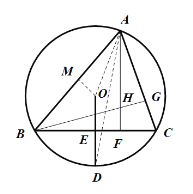
∵![]() ,∴
,∴![]() ,
,
∴![]()
∵![]() 为弧中点,
为弧中点,![]() ,
,
![]()
![]() ,
,
![]() ,
,
又∵![]()
![]() (AAS),
(AAS),
∴![]() .
.
∴![]() .
.
(3)连接![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,
,

由(2)可知,![]() ,
,![]() ,
,
∴四边形![]() 是菱形
是菱形
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]()
![]() (SAS),
(SAS),
∴![]()
![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]()
![]() ,
,
∴![]()
![]() 四边形
四边形![]() 内接于
内接于![]() ,
,
则有:![]() ,
,
∴![]()
![]() (SAS).
(SAS).
![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
又∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
则由勾股定理可求得:![]() .
.
∴![]() ,
,
又![]() ,
,
∴![]()
即![]()
∴![]()
解得![]() ,
,
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() ;当自变量
;当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() .探究过程如下,请补充完整.
.探究过程如下,请补充完整.
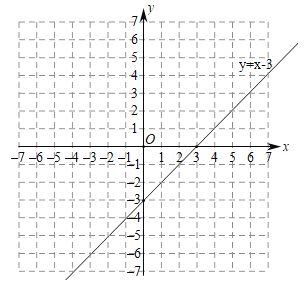
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有三个交点,则
有三个交点,则![]() ;
;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]()
![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
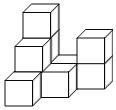
【题目】如图,在一次数学活动课上,张明用10个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要______个小立方体,王亮所搭几何体的表面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=90°,AB=8,CB=5,动点M从C点开始沿CB运动,动点N从B点开始沿BA运动,同时出发,两点均以1个单位/秒的速度匀速运动(当M运动到B点即同时停止),运动时间为t秒.
(1)AN= ;CM= .(用含t的代数式表示)
(2)连接CN,AM交于点P.
①当t为何值时,△CPM和△APN的面积相等?请说明理由.
②当t=3时,试求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
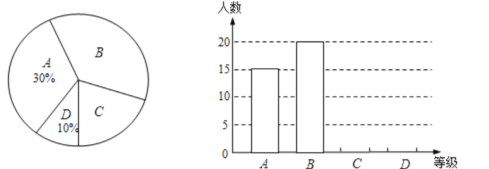
⑴ 九年级(1)班参加体育测试的学生有_________人;
⑵ 将条形统计图补充完整;
⑶ 在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
⑷ 若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有___人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
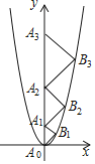
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角顶点在抛物线上的等腰直角三角形,则
都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为________.
的斜边长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com