
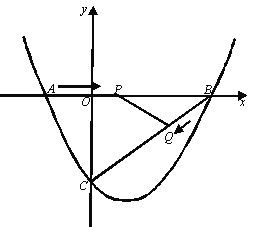
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A(
与x轴交于点A(![]() ,0)、B(4,0)两点,与y轴交于点C。
,0)、B(4,0)两点,与y轴交于点C。
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动。其中一个点到达终点时,另一个点也停止运动。当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最多面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK∶S△PBO=5∶2,求K点坐标。
【答案】(1)、y=![]() ;(2)、t=1时,最大面积为
;(2)、t=1时,最大面积为![]() ;(3)、K1(1,﹣
;(3)、K1(1,﹣![]() ),K2(3,﹣
),K2(3,﹣![]() ).
).
【解析】试题分析:(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=-![]() (t-1)2+
(t-1)2+![]() .利用二次函数的图象性质进行解答;
.利用二次函数的图象性质进行解答;
(3)利用待定系数法求得直线BC的解析式为y=![]() x-3.由二次函数图象上点的坐标特征可设点K的坐标为(m,
x-3.由二次函数图象上点的坐标特征可设点K的坐标为(m, ![]() m2-
m2-![]() m-3).
m-3).
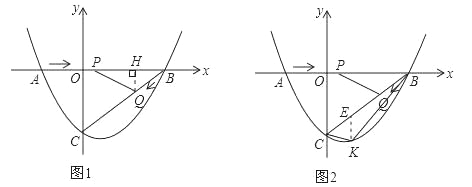
如图2,过点K作KE∥y轴,交BC于点E.结合已知条件和(2)中的结果求得S△CBK=![]() .则根据图形得到:S△CBK=S△CEK+S△BEK=
.则根据图形得到:S△CBK=S△CEK+S△BEK=![]() EKm+
EKm+![]() EK(4-m),把相关线段的长度代入推知:-
EK(4-m),把相关线段的长度代入推知:-![]() m2+3m=
m2+3m=![]() .易求得K1(1,-
.易求得K1(1,-![]() ),K2(3,-
),K2(3,-![]() ).
).
试题解析:(1)把点A(-2,0)、B(4,0)分别代入y=ax2+bx-3(a≠0),得
![]() ,
,
解得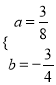 ,
,
所以该抛物线的解析式为:y=![]() x2-
x2-![]() x-3;
x-3;
(2)设运动时间为t秒,则AP=3t,BQ=t.
∴PB=6-3t.
由题意得,点C的坐标为(span>0,-3).
在Rt△BOC中,BC=![]() =5.
=5.
如图1,过点Q作QH⊥AB于点H.
∴QH∥CO,
∴△BHQ∽△BOC,
∴![]() ,即
,即![]() ,
,
∴HQ=![]() t.
t.
∴S△PBQ=![]() PBHQ=
PBHQ=![]() (6-3t)
(6-3t)![]() t=-
t=-![]() t2+
t2+![]() t=-
t=-![]() (t-1)2+
(t-1)2+![]() .
.
当△PBQ存在时,0<t<2
∴当t=1时,
S△PBQ最大=![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是![]() ;
;
(3)设直线BC的解析式为y=kx+c(k≠0).
把B(4,0),C(0,-3)代入,得
![]() ,
,
解得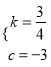 ,
,
∴直线BC的解析式为y=![]() x-3.
x-3.
∵点K在抛物线上.
∴设点K的坐标为(m, ![]() m2-
m2-![]() m-3).
m-3).
如图2,过点K作KE∥y轴,交BC于点E.则点E的坐标为(m, ![]() m-3).
m-3).
∴EK=![]() m-3-(
m-3-(![]() m2-
m2-![]() m-3)=-
m-3)=-![]() m2+
m2+![]() m.
m.
当△PBQ的面积最大时,∵S△CBK:S△PBQ=5:2,S△PBQ=![]() .
.
∴S△CBK=![]() .
.
S△CBK=S△CEK+S△BEK=![]() EKm+
EKm+![]() EK(4-m)
EK(4-m)
=![]() ×4EK
×4EK
=2(-![]() m2+
m2+![]() m)
m)
=-![]() m2+3m.
m2+3m.
即:-![]() m2+3m=
m2+3m=![]() .
.
解得 m1=1,m2=3.
∴K1(1,-![]() ),K2(3,-
),K2(3,-![]() ).
).


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
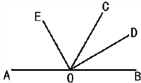
【题目】如图,点O在直线AB上,OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度数;
(3)射线OD与OE之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式:__________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)琪琪用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运20千克,A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 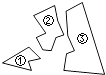
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,每个小正方形的顶点称为格点.我们将从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换.
的另一个格点的运动称为一次跳马变换.
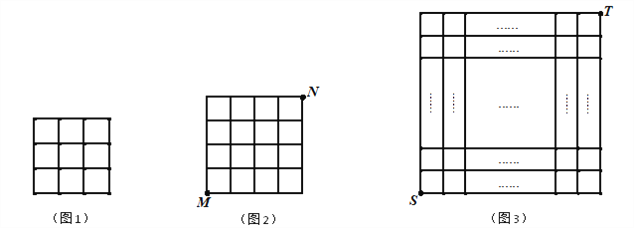
(1)在图1中画出边长为![]() 的正方形,使它的顶点在网格的格点上.
的正方形,使它的顶点在网格的格点上.
(2)在图2中有一只电子小马从格点![]() 出发,经过跳马变换到达与其相对的格点
出发,经过跳马变换到达与其相对的格点![]() ,则最少需要跳马变换的次数是 次.
,则最少需要跳马变换的次数是 次.
(3)如图3,在![]() 的正方形网格中,一只电子小马从格点
的正方形网格中,一只电子小马从格点![]() 经过若干次跳马变换到达与其相对的格点
经过若干次跳马变换到达与其相对的格点![]() ,则它跳过的最短路程为 .
,则它跳过的最短路程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com