Question

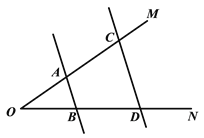
【题目】问题情境：如图，∥，，，求的度数.

小明的思路是过点作∥，通过平行线的性质来求.

（1）按照小明的思路，求的度数；

（2）问题迁移：如图，∥，点在射线上运动，记，，当点在、两点之间运动时，问与、之间有何数量关系？请说明理由；

（3）在（2）的条件下，如果点不在、两点之间运动时（点与点、、三点不重合），请直接写出与、之间的数量关系.

Answer 1

【答案】（1）110°（2）（3）①当点在左侧时，； ②当点在右侧时，

【解析】分析：（1）过P作PE∥AB，通过平行线性质可得∠A+∠APE=180°，∠C+∠CPE=180°再代入∠PAB=130°，∠PCD=120°可求∠APC即可；

（2）过P作PE∥AD交AC于E，推出AB∥PE∥DC，根据平行线的性质得出∠α=∠APE，∠β=∠CPE，即可得出答案；

（3）分两种情况：P在BD延长线上；P在DB延长线上，分别画出图形，根据平行线的性质得出∠α=∠APE，∠β=∠CPE，即可得出答案．

详解：∵AB∥CD，

∴PE∥AB∥CD，

∴∠A+∠APE=180,∠C+∠CPE=180，

∵∠PAB=130,∠PCD=120，

∴∠APE=50,∠CPE=60，

∴∠APC=∠APE+∠CPE=110.

(2)∠APC=∠α+∠β，

理由：如图2,过P作PE∥AB交AC于E，

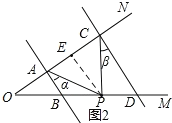
∵AB∥CD，

∴AB∥PE∥CD，

∴∠α=∠APE，∠β=∠CPE，

∴∠APC=∠APE+∠CPE=∠α+∠β；

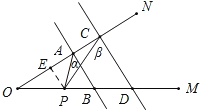
(3)如图所示，当P在BD延长线上时，∠CPA=∠α∠β；

如图所示，当P在DB延长线上时，∠CPA=∠β∠α.