【题目】计算（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
（9）
（10）
【答案】（1）-1；（2）-2.12；（3）
；（4）0；（5）
；（6）
；（7）-3；（8）
；（9）5；（10）0
【解析】
（1）根据有理数加法法则直接计算即可；
（2）先化简绝对值，再把减法变成加法计算即可；
（3）根据有理数乘法法则直接计算即可；
（4）几个含0的有理数相乘结果为0；
（5）先计算括号里面的，然后再算减法即可；
（6）把
换成
，再用有理数乘法的分配律计算即可；
（7）先把减法变成加法，在按有理数加法计算即可；
（8）按照有理数乘法法则计算即可；
（9）先用有理数乘法分配律，然后再进行有理数加减运算即可；
（10）用有理数乘法分配律的逆运算计算即可.
解：（1）原式=
=-1；
（2）原式=-3.52+1.4=-2.12；
（3）原式=
=；
（4）原式=0；
（5）原式=
=
=；
（6）原式=
=
=
=；
（7）原式=
=
=
=-3；
（8）原式=
=
（9）原式=
=
=5；
（10）原式=
=
=0
科目：初中数学 来源： 题型：
【题目】“雄安新区”是中共中央作出“千年大计、国家大事”的重大决策。雄安新区位于北京、天津和保定构成的一个等边三角形腹地，距离北京、天津和保定市分别为105公里、105公里、30公里，如图所示。现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,己知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km，北京与天津的里程为135km,求城际特快列车的速度是多少km/h？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数填在相应的大括号里：
﹣5.
，|﹣
|，0.5252252225…，0，﹣0.6363，﹣（﹣1）2007，1
，23%，﹣π
正数集合：{ }
负数集合：{ }
整数集合：{ }
分数集合：{ }
无理数集合：{ }
非负数集合：{ }
查看答案和解析>>
科目：初中数学 来源： 题型：
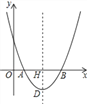
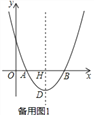
【题目】如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2﹣10ax+16a（a≠0）交x轴于A、B两点，抛物线的顶点为D，对称轴与x轴交于点H，且AB=2DH．
（1）求a的值；
（2）点P是对称轴右侧抛物线上的点，连接PD，PQ⊥x轴于点Q，点N是线段PQ上的点，过点N作NF⊥DH于点F，NE⊥PD交直线DH于点E，求线段EF的长；
（3）在（2）的条件下，连接DN、DQ、PB，当DN=2QN（NQ＞3），2∠NDQ+∠DNQ=90°时，作NC⊥PB交对称轴左侧的抛物线于点C，求点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某欢乐谷为回馈广大谷迷，在暑假期间推出学生个人门票优惠价，各票价如下：
票价种类 | （A）学生夜场票 | （B）学生日通票 | （C）节假日通票 |
单价（元） | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生，其中购买的B种票数是A种票数的3倍还多7张，C种票y张．
（1）直接写出y与x之间的函数关系式；
（2）设购票总费用为w元，求w（元）与x（张）之间的函数关系式；
（3）为方便学生游玩，计划购买的学生夜场票不低于20张，且每种票至少购买5张，则有几种购票方案？并指出哪种方案费用最少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）+5，-3，+10，-8，-6，+12，-10
（1）守门员最后是否回到了球门线的位置？
（2）在练习过程中，守门员离开球门最远距离是多少米？
（3）守门员全部练习结束后，他共跑了多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察与思考：阅读下列材料，并解决后面的问题
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作AD⊥BC于D（如图（1）），则
，即AD=csinB，AD=bsinC，于是csinB=bsinC，即
，同理有： 
，所以
．
即：在一个锐角三角形中，各边和它所对角的正弦的比相等在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．
根据上述材料，完成下列各题．
（1）如图（2），△ABC中，∠B=45°，∠C=75°，BC=60，则∠A= ；AC= ；
（2）某次巡逻中，如图（3），我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上，随后以40海里/时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在的北偏西75°的方向上，求此时渔政船距钓鱼岛A的距离AB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知a，b为实数，下列说法：①若a，b互为相反数，则
＝﹣1；②若a+b＜0，ab＞0，则|2a+b|＝﹣2a﹣b；③若|a|＞|b|，则（a+b）（a﹣b）是正数；其中正确的有（ ）个．
A.0B.1C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简,再求值：
阅读材料，大数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+
，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…
＝？
观察下面三个特殊的等式
将这三个等式的两边相加，可以得到1×2+2×3+3×4＝
读完这段材料，请你思考后回答：（只需写出结果，不必写中间的过程）
（1）
（2）1×2＋2×3＋3×4＋…＋n×(n+1)=
（3）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com