Question

如图，一次函数分别交y轴、x轴于A、B两点，抛物线y=﹣x²+bx+c过A、B两点．

（1）求这个抛物线的解析式；

（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？

（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

 

Answer 1

【答案】

（1）y=﹣x²+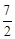x+2（2）当t=2时，MN有最大值4（3）D点坐标为（0，6），（0，﹣2）或（4，4）

【解析】解：（1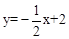）∵分别交y轴、x轴于A、B两点，

∴A、B点的坐标为：A（0，2），B（4，0）。

将x=0，y=2代入y=﹣x²+bx+c得c=2；

将x=4，y=0代入y=﹣x²+bx+c得0=﹣16+4b+2，解得b=。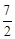

∴抛物线解析式为：y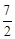=﹣x²+x+2。

（2）如图1，

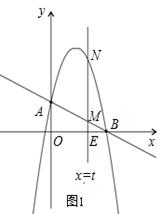
设MN交x轴于点E，则E（t，0），BE=4﹣t。

∵，

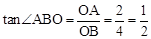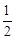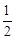∴ME=BE•tan∠ABO=（4﹣t）× =2﹣t。

又∵N点在抛物线上，且x_N=t，∴y_N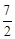=﹣t²+t+2。

∴。

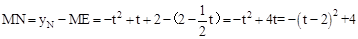∴当t=2时，MN有最大值4。

（3）由（2）可知，A（0，2），M（2，1），N（2，5）．

如图2，

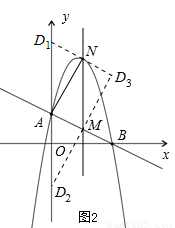
以A、M、N、D为顶点作平行四边形，D点的可能位置有三种情形。

（i）当D在y轴上时，设D的坐标为（0，a），

由AD=MN，得|a﹣2|=4，解得a₁=6，a₂=﹣2，

从而D为（0，6）或D（0，﹣2）。

（ii）当D不在y轴上时，由图可知D为D₁N与D₂M的交点，

由D₁（0，6），N（2，5）易得D₁N的方程为y=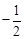x+6；

由D₂（0，﹣2），M（2，1）D₂M的方程为y=x﹣2。

由两方程联立解得D为（4，4）。

综上所述，所求的D点坐标为（0，6），（0，﹣2）或（4，4）。

（1）首先求得A、B点的坐标，然后利用待定系数法求抛物线的解析式。

（2）求得线段MN的表达式，这个表达式是关于t的二次函数，利用二次函数的极值求线段MN的最大值。

（3）明确D点的可能位置有三种情形，如图2所示，不要遗漏．其中D₁、D₂在y轴上，利用线段数量关系容易求得坐标；D₃点在第一象限，是直线D₁N和D₂M的交点，利用直线解析式求得交点坐标。