
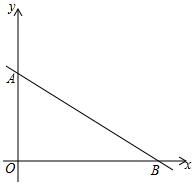
 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.分析 (1)根据坐标轴上点的坐标特征可求得A、B的坐标,用m表示出点P的坐标,利用面积可求得m的值,进一步求得P点坐标;
(2)可用t表示出BP、AP的长,分AP=AO、AP=OP和OP=AO三种情况,分别得到关于t的方程,可求得t的值.
解答 解:(1)当x=0时,y=6,
当y=0时,x=8,
则A(0,6),B(8,0),
AB=10,
设点P的坐标为(m,-$\frac{3}{4}$m+6),
∵△OPA的面积为12,
∴$\frac{1}{2}$×6×|m|=12,
解得:m=±4,
∴点P的坐标为(-4,9)或(4,3).
(2)由题意可知BP=t,AP=10-t,
当△AOP为等腰三角形时,有AP=AO、AP=OP和AO=OP三种情况.
①当AP=AO时,则有10-t=6,可解得t=4;
②当AP=OP时,过P作PM⊥AO,垂足为M,如图1,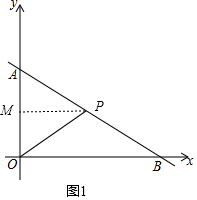
则M为AO中点,故P为AB中点,此时t=5;
③当AO=OP时,过O作ON⊥AB,垂足为N,过P作PH⊥OB,垂足为H,如图2,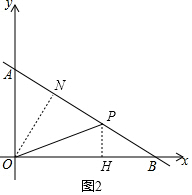
则AN=$\frac{1}{2}$AP=$\frac{1}{2}$(10-t),
∵PH∥AO,
∴△AOB∽△PHB,
∴$\frac{PB}{PH}$=$\frac{AB}{AO}$,即$\frac{t}{PH}$=$\frac{10}{6}$,
∴PH=$\frac{3}{5}$t,
又∠OAN+∠AON=∠OAN+PBH=90°,
∴∠AON=∠PBH,且∠ANO=∠PHB,
∴△ANO∽△PHB,
∴$\frac{PB}{AO}$=$\frac{PH}{AN}$,即$\frac{t}{6}$=$\frac{\frac{3}{5}}{\frac{1}{2}(10-t)}$,解得t=$\frac{14}{5}$.
综上可知当t的值为4、5和$\frac{14}{5}$时,△AOP为等腰三角形.
点评 本题主要考查一次函数的综合应用,涉及知识点有坐标轴上点的坐标特征,等腰三角形的性质,在(2)中分三种情况讨论,考查知识点较多,综合性较强,但所考查知识比较基础,难度适中.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
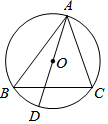 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的钟表,表盘上均匀分布着60条刻度线,若时针和分针分别指向两条相邻的刻度线,则钟表在0点-12点中所表示的时间可能是2点12分或9点48分.
如图所示的钟表,表盘上均匀分布着60条刻度线,若时针和分针分别指向两条相邻的刻度线,则钟表在0点-12点中所表示的时间可能是2点12分或9点48分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm、3cm、5cm | B. | 5cm、6cm、10cm | C. | 1cm、1cm、3cm | D. | 3cm、4cm、9cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com