
| 13 | 4 |
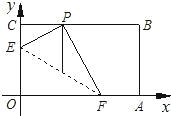 求证明)
求证明) 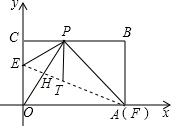 解:(1)设OE=y,则CE=3-y,
解:(1)设OE=y,则CE=3-y,| 13 |
| 6 |
| 13 |
| 4 |
| 13 |
| 6 |
| 13 |
| 4 |
| 2x |
| 3 |
| 13 |
| 6 |
| OH•OP |
| OC |
| (x2+9) |
| 6 |
| x2 |
| 6 |
| 3 |
| 2 |
| x2 |
| 6 |
| 3 |
| 2 |
| 5x |
| 3 |
| (x2+9) |
| 6 |
| 5 |
| 3 |
5
| ||
| 3 |


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
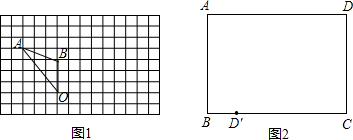
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的(不计接缝)(如图1).
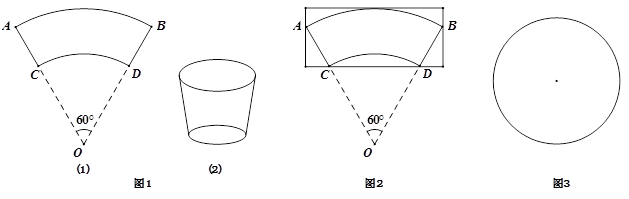
(1)求纸杯的底面半径和侧面积(结果保留π)
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片
(3)如图3,若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面,最多能裁出多少个?
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
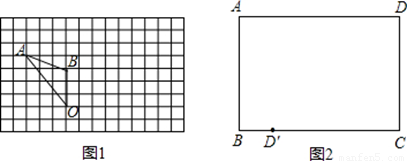
①如图1,在每个小方格都是边长为1个单位长度的正方形方格纸中有△OAB,
请将△OAB绕点O顺时针旋转90°,画出旋转后的△OA’B’;
②折纸:有一张矩形纸片ABCD(如图2),要将点D沿某条直线翻折180°,恰好落在BC边上的点D’
处,,请在图中作出该直线。
查看答案和解析>>
科目:初中数学 来源:2012届江苏省无锡锡山区九年级下学期期中考试数学卷(解析版) 题型:解答题
某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的(不计接缝)(如图1).

(1)求纸杯的底面半径和侧面积(结果保留π)
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片
(3)如图3,若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面,最多能裁出多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com