
【题目】已知点![]() 的坐标为
的坐标为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 的中点,双曲线
的中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
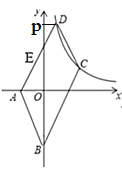
(2)如图1,点![]() 在
在![]() 轴上,若四边形
轴上,若四边形![]() 是平行四边形,求点
是平行四边形,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,动点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,试求满足要求的所有点
为顶点的四边形为平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ;
;![]() 、
、![]() 或、
或、![]() 、
、![]()
【解析】
(1) 过点![]() 作
作![]() 轴于
轴于![]() ,再证
,再证![]() ,即可求出
,即可求出![]() 、
、![]() 、
、![]() 的值;
的值;
(2) 设![]() 得到
得到![]() ,即可求出点
,即可求出点![]() 的坐标;
的坐标;
(3)由反比例函数的解析式为![]() ,再由点P在双曲线
,再由点P在双曲线![]() 上,点Q在y轴上,设Q(0,y), P(x,
上,点Q在y轴上,设Q(0,y), P(x, ![]() ),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
解:(1)过点![]() 作
作![]() 轴于
轴于![]()
∵![]() 为
为![]() 的中点,
的中点,
∴DE=AE,
又∵∠PED=∠OEA, ∠DPE=∠AOE,
∴![]()
∴![]()
∴![]()
![]()
∴![]() 即
即![]()
∴![]()
(2)∵四边形![]() 是平行四边形.
是平行四边形.
∴![]()
∵![]()
![]()
![]()
![]() 在
在![]() 轴上
轴上
∴设![]()
则![]()
![]()
∴![]()
(3)∵反比例函数的表达式为![]() ,
,
∵点P在双曲线![]() 上,点Q在y轴上,
上,点Q在y轴上,
∴设![]() );
);
①AB为边时,如图①所示.若四边形ABPQ平行四边形,
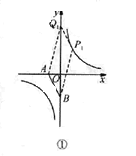
则![]() =0,解得x=1,此时P1(1,4),Q1(0,6);
=0,解得x=1,此时P1(1,4),Q1(0,6);
如图②所示.
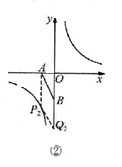
若四边形ABQP是平行四边形,则x=1.此时P2(1,4),Q2(0,6);
②当AB为对角线时,如图③所示,
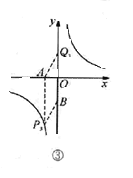
AP=BQ,且AP//BQ,
所以x=1,
所以P3(1,4),Q3(0,2),
故满足要求的点P,Q的坐标分别是![]() 、
、![]() ;
;![]() 、
、![]() 或、
或、![]() 、
、![]()
.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β;②α-β;③β-α;④180°-α-β中.∠AEC的度数可能是 _____(把正确答案的序号填在横线上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划在某商店购买秋季运动会的奖品,若买5个篮球和10个足球需花费1150元,若买9个篮球和6个足球需花费1170元.
(1)篮球和足球的单价各是多少元?
(2)实际购买时,正逢该商店进行促销.所有体育用品都按原价的八折优惠出售,学校购买了若干个篮球和足球,恰好花费1760元.请直接写出学校购买篮球和足球的个数各是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:
①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④4ac<b2
其中正确的个数有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100)
+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() (x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(1)求直线l的函数解析式;
(2)过点P作直线l的垂线l1 , 交函数y= ![]() (x>0)图象于点C,求△OPC的面积.
(x>0)图象于点C,求△OPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.
(1)如图1,求∠DAO的大小及线段DE的长;
(2)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3 ![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com