
 如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.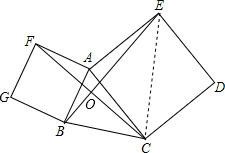 证明:(1)∵四边形ACDE、BAFG都是正方形,
证明:(1)∵四边形ACDE、BAFG都是正方形,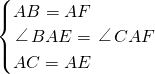 ,
,

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
| 2 |
 ,这时我们把关于x的形如ax2+
,这时我们把关于x的形如ax2+| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•龙岗区模拟)如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
(2013•龙岗区模拟)如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

 ,这时我们把关于x的形如
,这时我们把关于x的形如 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”. 必有实数根;
必有实数根; 的一个根,且四边形ACDE的周长是6
的一个根,且四边形ACDE的周长是6 ,求△ABC面积.
,求△ABC面积.查看答案和解析>>
科目:初中数学 来源:2009-2010学年北京市海淀区九年级(上)期中数学试卷(解析版) 题型:解答题
 ,这时我们把关于x的形如
,这时我们把关于x的形如 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”. 必有实数根;
必有实数根; 的一个根,且四边形ACDE的周长是6
的一个根,且四边形ACDE的周长是6 ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com