
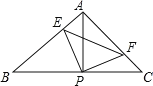
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交边AB,AC于点E,F,当∠EPF在△ABC所在平面内绕顶点P转动时(点E不与A,B重合),给出以下四个结论:①△PFA≌△PEB②EF=AP③△PEF是等腰直角三角形④S四边形AEPF![]() S△ABC,上述结论中始终正确有______.
S△ABC,上述结论中始终正确有______.
【答案】①③④
【解析】
由等腰直角三角形的性质得AP![]() BC=PB,∠B=∠CAP=45°,根据余角的性质得∠BPE=∠APF,进而即可证明△PFA≌△PEB,即可判断①;根据等腰三角形的性质和中位线的性质,即可判断②;由△PFA≌△PEB得PE=PF,进而即可判断③;由△PFA≌△PEB,得S△PFA=S△PEB,进而即可判断④.
BC=PB,∠B=∠CAP=45°,根据余角的性质得∠BPE=∠APF,进而即可证明△PFA≌△PEB,即可判断①;根据等腰三角形的性质和中位线的性质,即可判断②;由△PFA≌△PEB得PE=PF,进而即可判断③;由△PFA≌△PEB,得S△PFA=S△PEB,进而即可判断④.
∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴AP⊥BC,AP![]() BC=PB,∠B=∠CAP=45°,
BC=PB,∠B=∠CAP=45°,
∵∠APF+∠EPA=90°,∠EAP+∠BPE=90°,
∴∠BPE=∠APF,
在△BPE和△APF中,
∵ ,
,
∴△PFA≌△PEB(ASA),即结论①正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP![]() BC,
BC,
又∵EF不一定是△ABC的中位线,
∴EF≠AP,故结论②错误;
∵△PFA≌△PEB,
∴PE=PF,
又∵∠EPF=90°,
∴△PEF是等腰直角三角形,故结论③正确;
∵△PFA≌△PEB,
∴S△PFA=S△PEB,
∴S四边形AEPF=S△APE+S△APF=S△APE+S△BPE=S△APB![]() S△ABC,故结论④正确;
S△ABC,故结论④正确;
综上,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),始终正确的有3个结论.
故答案为:①③④.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y![]() x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
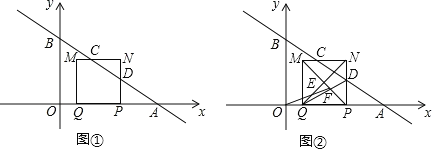
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y![]() x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;
(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() (0,
(0,![]() ),
),![]() (3,4).
(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点).若直线
两点).若直线![]() 与图象
与图象![]() 有公共点,结合函数图像,求点
有公共点,结合函数图像,求点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
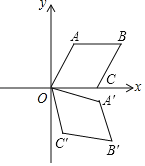
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC,点D,E分别在边AC,BC上,CD=CE,连接AE,点F,H,G分别为DE,AE,AB的中点连接FH,HG
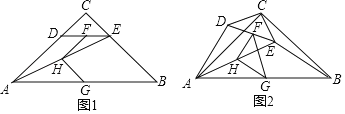
(1)观察猜想图1中,线段FH与GH的数量关系是 ,位置关系是
(2)探究证明:把△CDE绕点C顺时针方向旋转到图2的位置,连接AD,AE,BE判断△FHG的形状,并说明理由
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若CD=4,AC=8,请直接写出△FHG面积的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图像与x轴和y轴的正半轴分别交于A,B两点.已知OA+OB=6(O为坐标原点),且![]() =4,则这个一次函数的解析式为 ( )
=4,则这个一次函数的解析式为 ( )
A.y=-![]() x+2B.y=-2x+4
x+2B.y=-2x+4
C.y=![]() x+2D.y=-
x+2D.y=-![]() x+2或y=-2x+4
x+2或y=-2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
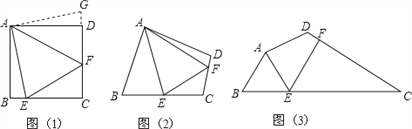
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() .小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得
.小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得![]() ,
,![]() .在进行如下操作时遇到了下面的几个问题,请你帮助解决.
.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
(1)将![]() 的顶点
的顶点![]() 移到矩形的顶点
移到矩形的顶点![]() 处,再将三角形绕点
处,再将三角形绕点![]() 顺时针旋转使
顺时针旋转使![]() 点落在
点落在![]() 边上,此时,
边上,此时,![]() 恰好经过点
恰好经过点![]() (如图
(如图![]() ),请你求出
),请你求出![]() 和
和![]() 的长度;
的长度;
(2)在(1)的条件下,小明先将三角形的边![]() 和矩形边
和矩形边![]() 重合,然后将
重合,然后将![]() 沿直线
沿直线![]() 向右平移,至
向右平移,至![]() 点与
点与![]() 重合时停止.在平移过程中,设
重合时停止.在平移过程中,设![]() 点平移的距离为
点平移的距离为![]() ,两纸片重叠部分面积为
,两纸片重叠部分面积为![]() ,求在平移的整个过程中,
,求在平移的整个过程中,![]() 与
与![]() 的函数关系式,并求当重叠部分面积为
的函数关系式,并求当重叠部分面积为![]() 时,平移距离
时,平移距离![]() 的值(如图
的值(如图![]() ).
).
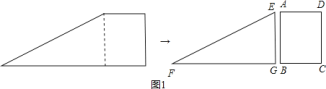
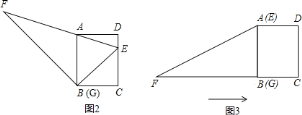
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com