
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() .点
.点![]() 为
为![]() 内一点,且
内一点,且![]() .
.
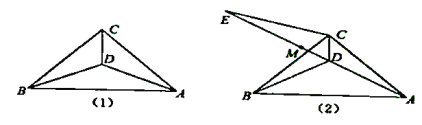
(1)求证:![]() ;
;
(2)![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() .如图(2),
.如图(2),
①求证:![]() 平分
平分![]() ;
;
②若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请判断
,请判断![]() 、
、![]() 的数量关系,并给出证明.
的数量关系,并给出证明.
【答案】(1)见详解;(2)①见详解;②ME=BD,理由见详解.
【解析】
(1)利用线段的垂直平分线的性质即可证明;
(2)①易证BD=AD,可得△ADC≌△BDC,即可求得∠ACD=∠BCD=45°即可解题;
②连接MC,易证△MCD为等边三角形,即可证明△BDC≌△EMC即可解题;
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,
∴BD=AD,
在△ADC和△BDC中,
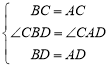 ,
,
∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
②解:结论:ME=BD,
理由:连接MC,
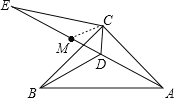
∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,
∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°
在△BDC和△EMC中,
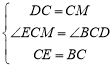 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD.


科目:初中数学 来源: 题型:
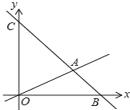
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究与证明)
在正方形ABCD中,G是射线AC上一动点(不与点A、C重合),连BG,作BH⊥BG,且使BH=BG,连GH、CH.
(1)若G在AC上(如图1),则:①图中与△ABG全等的三角形是 .
②线段AG、CG、GH之间的数量关系是 .
(2)若G在AC的延长线上(如图2),那么线段AG、CG、BG之间有怎样的数量关系?写出结论并给出证明;
(应用)(3)如图3,G在正方形ABCD的对角线CA的延长线上,以BG为边作正方形BGMN,若AG=2,AD=4,请直接写出正方形BGMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于点A(2,0),与反比例函数y=![]() 的图象交于点B(3,n).
的图象交于点B(3,n).
(1)求一次函数与反比例函数的表达式;
(2)若点P为x轴上的点,且△PAB的面积是2,则点P的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
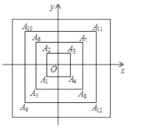
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8…顶点依次用A1,A2,A3,A4,…表示,则顶点A2019的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=50°,BD,CE是∠ABC,∠ACB的平分线,则∠BOC的度数为( )
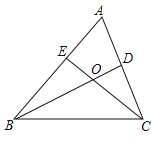
A.105°B.115°C.125°D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com