
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF .
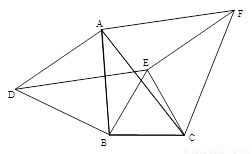
(1)将△CBA绕着点C旋转,可以与哪一个三角形重合,以及旋转的度数(直接写答案);
(2)四边形AFED一定是平行四边形吗?如果是,请说明理由;
(3)当△ABC满足什么条件时,四边形AFED一定是菱形.( 直接写答案,不必说明理由)
(1)△CEF, 顺时针60o(2) 是,理由见解析(3)AB=AC
【解析】(1)△CEF, 顺时针60o …………2分
(2) 四边形AFED是平行四边形 …………3分
∵△ABD、△BCE、△ACF为等边三角形
∴CB=CE,CA=CF, ∠BCE=∠ACF=60o
∴∠BCE-∠ACE=∠ACF-∠ACE即∠BCA=∠ECF
∴△ABC≌△FEC
∴AB=EF …………5分
又∵AB=AD ∴AD=FE
同理可证△ABC≌△DBE,BD=FA
∴四边形AFED是平行四边形 …………7分
(3)AB=AC …………8分
(1)根据等边三角形BEC和ACF,推出AC=CF,BC=CE,∠ECB=∠FCA=60°,求出∠ACB=∠FCE,根据SAS证△ABC和△FEC全等即可;
(2)由(1)推出AD=FE,同理求出△ABC≌DBE,推出BD=AF,根据平行四边形的判定推出即可;
(3)根据AB=AC和AB=EF,AC=AF,推出AD=DE=EF=AF,根据菱形的判定即可推出四边形AFED是菱形.


科目:初中数学 来源: 题型:
 19、如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.
19、如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:
 24、(1)如图,以△ABC三边向外分别作等边△ACD、△ABE、△BCF,判断四边形ADFE的形状;
24、(1)如图,以△ABC三边向外分别作等边△ACD、△ABE、△BCF,判断四边形ADFE的形状;查看答案和解析>>
科目:初中数学 来源: 题型:
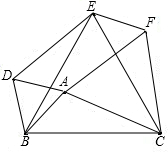 如图,以△ABC三边为边,分别作三个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC三边为边,分别作三个等边三角形,即△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:
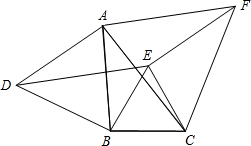 如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC三边为边在BC的同一侧分别作3个等边三角形,即△ABD、△BCE、△ACF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com