
【题目】已知关于x的二次函数![]() 的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
(1)求k的值;
(2)在(1)的条件下,若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(
的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(![]() ,
, ![]() ),S(
),S(![]() ,
, ![]() )中的纵坐标
)中的纵坐标![]() ,
, ![]() 分别是一元二次方程
分别是一元二次方程![]() 的解,求四边形AQBS的面积
的解,求四边形AQBS的面积![]() ;
;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数![]() 图象上的点P使得
图象上的点P使得![]() =2
=2![]() ,若存在,求出点P的坐标;若不存在,请说明理由.
,若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)![]() =
=![]() .
.
【解析】试题分析:(1)设A点坐标为(x1,0),B点坐标为(x2,0),由A、B两点关于原点对称,即可得x1+x2=0,又由x1+x2=-(k2-3k-4),即可求得k的值;
(2)由Q点的坐标求出m的值,从而确定一元二次方程y2-my-1=0即为y2+y-1=0,解得:y=![]() ,因为点R在点S的左边,所以yR=
,因为点R在点S的左边,所以yR=![]() ,yS=
,yS=![]() ,由(1)得二次函数y=x2-2,令x2-2=0,解得:x1=
,由(1)得二次函数y=x2-2,令x2-2=0,解得:x1=![]() ,x2=
,x2=![]()
,所以A(-![]() ,0),B(
,0),B(![]() ,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
(3)由抛物线的顶点坐标为(0,-2),假设满足条件的点P存在,由S△PAB=2S△RAB,可得点P的纵坐标,即可得即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB;
试题解析:
(1)由题意,设A(![]() ,0),B(
,0),B(![]() ,0),
,0),
则![]()
![]() =0,
=0, ![]()
![]() ,
,
∴![]() ,解得,即
,解得,即![]() ,或
,或![]() .
.
当![]() 时,二次函数是
时,二次函数是![]() 与
与![]() 轴无交点,故舍去.
轴无交点,故舍去.
∴![]()
(2)∵Q的坐标为(-1,-1),即![]() ,解得
,解得![]() ,
,
∴一元二次方程![]() 即为
即为![]() .
.
解这个方程, 且因点R在点S左边,
∴![]() ,
, ![]() .
.
由(1)得二次函数![]() ,令
,令![]() ,解得
,解得![]() ,
, ![]() ,
,
∴A(![]() ,0),B(
,0),B(![]() ,0).
,0).
![]() .
.
![]() =
=![]() +
+![]() =
=![]() +
+![]() =
=![]() +
+![]() =
=![]() .
.
设点P(x,y),
∵![]() =
=![]() ,
, ![]() =
=![]()
![]()
![]() ,
,
由![]() =
=![]() ,得
,得
![]() =
= ![]()
![]()
∴![]() =
=![]() ,
, ![]() .
.
又∵P必须在x轴的下方,
∴![]() ,但
,但![]() ,
, ![]() ,
,
而![]() ,
,
故这样的点P不存在。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的⊙
为半径的⊙![]() 交
交![]() 于点
于点![]() ,
, ![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
, ![]() ,
, ![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开州区城区2018年底已有绿化面积700公顷,响应“青山绿水就是金山银山”的号召,绿化面积逐年增加,预计到2020年底 绿化面积增加到1000公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
A.700(1+x)=1000B.700(1+x)2=1000
C.700(1+2x)=1000D.1000(1-x)2=700
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据直角三角形的判定的知识解决下列问题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
2014年北京市全年空气质量等级天数统计表
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?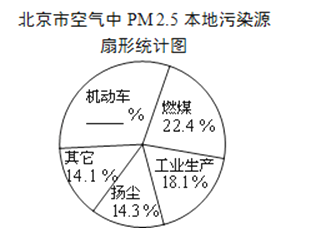
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com