
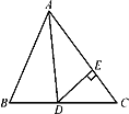
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
【答案】(1)∠ADBD=84°.
(2)∠ADE=60°.
【解析】试题分析:(1)已知∠B,∠C的度数,可求出三角形ABC中![]() BAC的度数,AD又是
BAC的度数,AD又是![]() BAC的角平分线,可以求得
BAC的角平分线,可以求得![]() BAD的值,从而在三角形ABD中即可求得∠ADB的度数。(2)由(1)可求得
BAD的值,从而在三角形ABD中即可求得∠ADB的度数。(2)由(1)可求得![]() CAD=
CAD=![]() BAD,若DE⊥AC,则在直角三角形中可以求得∠ADE的度数。
BAD,若DE⊥AC,则在直角三角形中可以求得∠ADE的度数。
试题解析:(1)∵在△ABC中,∠B=66°,∠C=54°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是∠BAC的平分线,
∴∠BAD=![]() ∠BAC=30°.
∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
(2)∵∠CAD=![]() ∠BAC=30°,DE⊥AC,
∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°.


科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
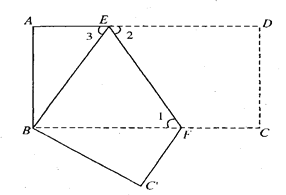
(1)折叠后,DC的对应线段是 ,CF的对应线段是 ;
(2)若∠1=50°,求∠2、∠3的度数;
(3)若CD=4,AD=6,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把a2﹣4a多项式分解因式,结果正确的是( )
A. a(a﹣4) B. (a+2)(a﹣2) C. a(a+2)(a﹣2) D. (a﹣2)2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对居民天然气收费采用阶梯气价,以“年度”作为一个阶梯气价结算周期,年度用气量分档和价格如下:第一档:年用气量0~242(含)立方米,价格a元/立方米,第二档:年用气量242~360(含)立方米,价格b元/立方米,即年用气量超过242度,超出部分气价按b元收费,某户居民一年用天然气300立方米,该户居民这一年应交纳天然气费是_____元.(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣3,﹣2),B(2,﹣2),C(3,1),D(﹣2,1)四个点.
(1)在图中描出A,B,C,D四个点,并顺次连接点A,B,C,D,A.
(2)直接写出线段AB,CD之间的关系.
(3)求四边形ABCD的面积. 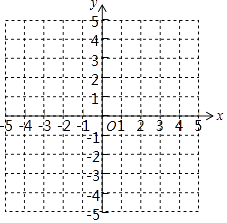
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=12cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
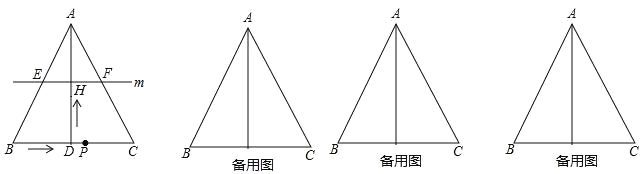
(1)连接DE、DF,当t为何值时,四边形AEDF为菱形?
(2)连接PE、PF,在整个运动过程中,△PEF的面积是否存在最大值?若存在,试求当△PEF的面积最大时,线段BP的长.
(3)是否存在某一时刻t,使点F在线段EP的中垂线上?若存在,请求出此时刻t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B(![]() ,n).
,n).
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=![]() 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com