
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x与反比例函数y=
x与反比例函数y= ![]() 在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).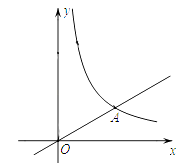
(1)求该反比例函数的关系式;
(2)将直线y= ![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;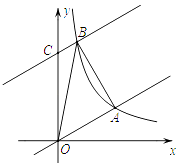
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
【答案】
(1)
解:∵点A(m,3)在直线y= ![]() x上
x上
∴3= ![]() m,
m,
∴m=3 ![]() ,
,
∴点A(3 ![]() ,3),
,3),
∵点A(3 ![]() ,3)在反比例函数y=
,3)在反比例函数y= ![]() 上,
上,
∴k=3 ![]() ×3=9
×3=9 ![]() ,
,
∴y= ![]()
(2)
解:直线向上平移8个单位后表达式为:y= ![]() x+8
x+8
∵AB⊥OA,直线AB过点A(3 ![]() ,3)
,3)
∴直线AB解析式:y=﹣ ![]() x+12,
x+12,
∴ ![]() x+8=﹣
x+8=﹣ ![]() x+12,
x+12,
∴x= ![]() .
.
∴B( ![]() ,9),
,9),
∴AB=4 ![]()
在Rt△AOB中,OA=6,
∴tan∠AOB= ![]()
(3)
解:∵△APB∽△ABO,
∴ ![]() ,
,
由(2)知,AB=4 ![]() ,OA=6
,OA=6
即 ![]()
∴AP=8,
∵OA=6,
∴OP=14,
过点A作AH⊥x轴于H
∵A(3 ![]() ,3),
,3),
∴OH=3 ![]() ,AH=3,
,AH=3,
在Rt△AOH中,
∴tan∠AOH= ![]() =
= ![]() =
= ![]() ,
,
∴∠AOH=30°
过点P作PG⊥x轴于G,
在Rt△APG中,∠POG=30°,OP=14,
∴PG=7,OG=7 ![]()
∴P(7 ![]() ,7).
,7).

【解析】(1)先确定出点A坐标,再用待定系数法求出反比例函数解析式;(2)先求出直线AB解析式,进而得出点B坐标秒即可得出结论;(3)利用相似三角形的性质得出AP,进而求出OP,再求出∠AOH=30°,最后用含30°的直角三角形的性质即可得出结论.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ) 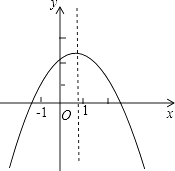
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F. 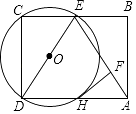
(1)求证:HF是⊙O的切线;
(2)若DH=3,AF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( ) 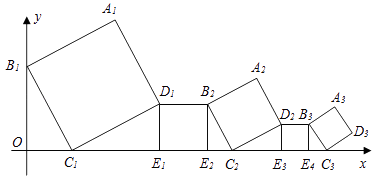
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
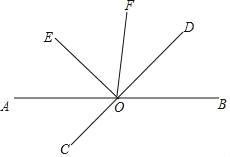
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题: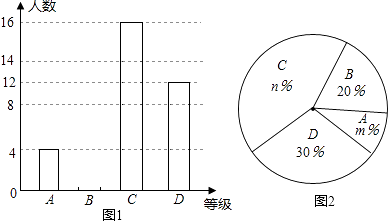
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com