
【题目】已知抛物线![]() (a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(1)求抛物线![]() 的函数解析式;
的函数解析式;
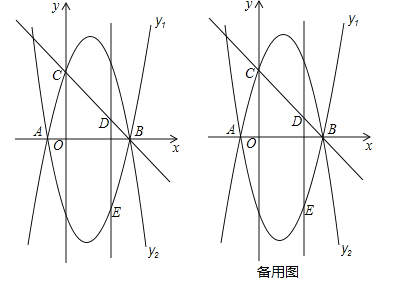
(2)如图①,将抛物线![]() 沿x轴翻折得到抛物线
沿x轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线
与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线![]() 于点E,求线段DE的长度的最大值;
于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线![]() 上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
【答案】(1)![]() ;(2)9;(3)(
;(2)9;(3)(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)将点A(﹣1,0)和点B(4,0)代入![]() 即可得到结论;
即可得到结论;
(2)由对称性可知,得到抛物线y2的函数解析式为![]() ,求得直线BC的解析式为:y=﹣x+4,设D(m,﹣m+4),E(m,
,求得直线BC的解析式为:y=﹣x+4,设D(m,﹣m+4),E(m,![]() ),其中0≤m≤4,得到DE=﹣m+4﹣(
),其中0≤m≤4,得到DE=﹣m+4﹣(![]() )=
)=![]() ,即可得到结论;
,即可得到结论;
(3)由题意得到△BOC是等腰直角三角形,求得线段BC的垂直平分线为y=x,由(2)知,直线DE的解析式为x=1,得到H(2,2),根据S⊙P:S△DFH=2π,得到r=![]() ,由于⊙P与直线BC相切,推出点P在与直线BC平行且距离为
,由于⊙P与直线BC相切,推出点P在与直线BC平行且距离为![]() 的直线上,于是列方程即可得到结论.
的直线上,于是列方程即可得到结论.
解:(1)将点A(﹣1,0)和点B(4,0)代入![]() 得:
得:
![]() 解得
解得![]() ,
,
∴抛物线y1的函数解析式为:![]() ;
;
(2)由对称性可知,抛物线y2的函数解析式为:![]() ,
,
∴C(0,4),
设直线BC的解析式为:y=kx+q,
把B(4,0),C(0,4)代入得,k=﹣1,q=4,
∴直线BC的解析式为:y=﹣x+4,设D(m,﹣m+4),E(m,![]() ),其中0≤m≤4,
),其中0≤m≤4,
∴DE=﹣m+4﹣(![]() )=
)=![]() ,
,
∵0≤m≤4,
∴当m=1时,DEmax=9;
此时,D(1,3),E(1,﹣6);
(3)由题意可知,△BOC是等腰直角三角形,
∴线段BC的垂直平分线为:y=x,由(2)知,直线DE的解析式为:x=1,
∴F(1,1),
∵H是BC的中点,
∴H(2,2),
∴DH=![]() ,FH=
,FH=![]() ,
,
∴S△DFH=1,设⊙P的半径为r,
∵S⊙P:S△DFH=2π,
∴r=![]() ,
,
∵⊙P与直线BC相切,
∴点P在与直线BC平行且距离为![]() 的直线上,
的直线上,
∴点P在直线y=﹣x+2或y=﹣x+6的直线上,
∵点P在抛物线![]() 上,
上,
∴![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() ,
,
![]() ,
,
解得:x3=![]() ,x4=
,x4=![]() ,
,
∴符合条件的点P坐标有4个,分别是(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别为坐标轴上的三个点,且
分别为坐标轴上的三个点,且![]() ,
,![]() ,
,![]() .
.
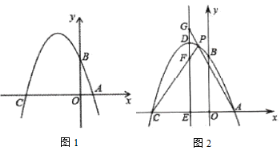
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 是抛物线上一个动点,且在直线
是抛物线上一个动点,且在直线![]() 的上方,连接
的上方,连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点,使四边形
,那么是否存在点,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,过抛物线顶点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),直线
两点重合),直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.

(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
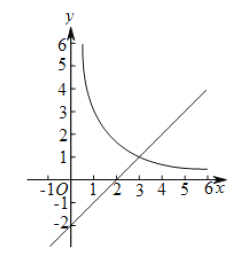
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( )
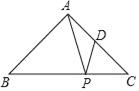
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点A作AD平分∠BAC交⊙O于点D,过点D作BC的平行线分别交AC、AB的延长线于点E、F,DG⊥AB于点G,连接BD.
(1)求证:△AED∽△DGB;
(2)求证:EF是⊙O的切线;
(3)若![]() ,OA=4,求劣弧
,OA=4,求劣弧![]() 的长度(结果保留π).
的长度(结果保留π).
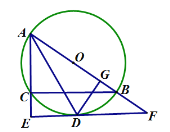
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com