
 须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
须是两人都在信号覆盖范围内方可进行,否则,手机无法联系. 解:(1)作辅助线PD⊥BC于D;
解:(1)作辅助线PD⊥BC于D; =10
=10 (千米)
(千米) =20
=20 (千米)
(千米) ,
, -30t,
-30t, -30t≥0,
-30t≥0, ;
; 小时有信号,
小时有信号, -30)÷30≈0.155(小时),合9分钟.
-30)÷30≈0.155(小时),合9分钟. 求出AP,从而求出s与t之间的函数关系式并写出自变量t的取值范围;
求出AP,从而求出s与t之间的函数关系式并写出自变量t的取值范围;

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
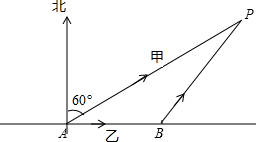 须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,
, )
)
查看答案和解析>>
科目:初中数学 来源:2009-2010学年重庆市南开中学九年级(上)月考数学试卷(9月份)(解析版) 题型:解答题
 ,
, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com