
【题目】问题背景:
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD.
CD.
简单应用:
(1)在图①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= ![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
【答案】
(1)3
(2)
解:连接AC、BD、AD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵ ![]() ,
,
∴AD=BD,
将△BCD绕点D,逆时针旋转90°到△AED处,如图③
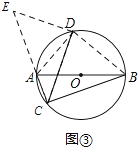 ,
,
∴∠EAD=∠DBC,
∵∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∵AB=13,BC=12,
∴由勾股定理可求得:AC=5,
∵BC=AE,
∴CE=AE+AC=17,
∵∠EDA=∠CDB,
∴∠EDA+∠ADC=∠CDB+∠ADC,
即∠EDC=∠ADB=90°,
∵CD=ED,
∴△EDC是等腰直角三角形,
∴CE= ![]() CD,
CD,
∴CD= ![]()
(3)
解:以AB为直径作⊙O,连接OD并延长交⊙O于点D1,连接D1A,D1B,D1C,如图④
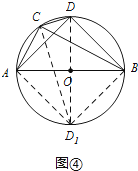
由(2)的证明过程可知:AC+BC= ![]() D1C,
D1C,
∴D1C= ![]() ,
,
又∵D1D是⊙O的直径,
∴∠DCD1=90°,
∵AC=m,BC=n,
∴由勾股定理可求得:AB2=m2+n2,
∴D1D2=AB2=m2+n2,
∵D1C2+CD2=D1D2,
∴CD=m2+n2﹣ ![]() =
= ![]() ,
,
∵m<n,
∴CD= ![]() ;
;
(4)[ "解:当点E在直线AC的左侧时,如图⑤ ![]() ,
,
连接CQ,PC,
∵AC=BC,∠ACB=90°,
点P是AB的中点,
∴AP=CP,∠APC=90°,
又∵CA=CE,点Q是AE的中点,
∴∠CQA=90°,
设AC=a,
∵AE= ![]() AC,
AC,
∴AE= ![]() a,
a,
∴AQ= ![]() AE=
AE= ![]() ,
,
由勾股定理可求得:CQ= ![]() a,
a,
由(2)的证明过程可知:AQ+CQ= ![]() PQ,
PQ,
∴ ![]() PQ=
PQ= ![]() a+
a+ ![]() a,
a,
∴ ![]() PQ=
PQ= ![]() AC;
AC;
当点E在直线AC的右侧时,如图⑥![]() 【解析】解:(1)由题意知:AC+BC=
【解析】解:(1)由题意知:AC+BC= ![]() CD,
CD,
∴3 ![]() +2
+2 ![]() =
= ![]() CD,
CD,
∴CD=3,;
(1)由题意可知:AC+BC= ![]() CD,所以将AC与BC的长度代入即可得出CD的长度;(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1 , 由(2)问题可知:AC+BC=
CD,所以将AC与BC的长度代入即可得出CD的长度;(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1 , 由(2)问题可知:AC+BC= ![]() CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.本题考查圆的综合问题,每一问都紧扣着前一问的结论,涉及勾股定理、圆周角定理,旋转的性质等知识,解题的关键是就利用好已证明的结论来进行解答,考查学生综合运用知识的能力.
CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.本题考查圆的综合问题,每一问都紧扣着前一问的结论,涉及勾股定理、圆周角定理,旋转的性质等知识,解题的关键是就利用好已证明的结论来进行解答,考查学生综合运用知识的能力.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣3x+k=0有两个实数根x1和x2
(1)求实数k的取值范围;
(2)若|x1﹣x2|=3﹣x1x2时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 ![]() BF长为半径画弧,两弧交于一点P,连
BF长为半径画弧,两弧交于一点P,连
接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 , ∠ABC=°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( ) 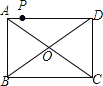
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”. 
(1)直接写出函数y= ![]() 图象上的所有“整点”A1 , A2 , A3 , …的坐标;
图象上的所有“整点”A1 , A2 , A3 , …的坐标;
(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com