
【题目】如图,等边![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交边
交边![]() 于点
于点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段;(不再另外添加辅助线)
相等的两条线段;(不再另外添加辅助线)
(2)探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形?并判断四边形
是平行四边形?并判断四边形![]() 是什么特殊的平行四边形,请说明理由;
是什么特殊的平行四边形,请说明理由;
(3)在(2)的条件下,以点![]() 为圆心,
为圆心,![]() 为半径作圆,根据
为半径作圆,根据![]() 与平行四边形
与平行四边形![]() 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由平行易得△BFE是等边三角形,那么各边是相等的;
(2)当点E是BC的中点时,△PEC为等边三角形,可得到PC=EC=BE=EF,也就得到了四边形EFPC是平行四边形,再有EF=EC可证为菱形;
(3)根据各点到圆心的距离作答即可.
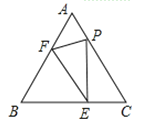
解:(1)如图,∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°.
又∵EF∥AC,
∴∠BFE=∠A=60°,∠BEF=∠C=60°,
∴△BFE是等边三角形,PE=EB,
∴EF=BE=PE=BF;
(2)当点E是BC的中点时,四边形是菱形;
∵E是BC的中点,
∴EC=BE,
∵PE=BE,
∴PE=EC,
∵∠C=60°,
∴△PEC是等边三角形,
∴PC=EC=PE,
∵EF=BE,
∴EF=PC,
又∵EF∥CP,
∴四边形EFPC是平行四边形,
∵EC=PC=EF,
∴平行四边形EFPC是菱形;
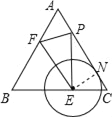
(3)如图所示:
当点E是BC的中点时,EC=1,则NE=ECcos30°=![]() ,
,
当0<r<![]() 时,有两个交点;
时,有两个交点;
当r=![]() 时,有四个交点;
时,有四个交点;
当![]() <r<1时,有六个交点;
<r<1时,有六个交点;
当r=1时,有三个交点;
当r>1时,有0个交点.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式![]() ,........请按照上述三个等式及其变化过程,回答下列问题。
,........请按照上述三个等式及其变化过程,回答下列问题。
(1)猜想![]() ________________.
________________.
(2)猜想_____________________=![]() .
.
(3)试猜想第N个等式为_____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) .
.
(2)(﹣2a)3﹣(﹣a)(3a)2.
(3)(x+2)2﹣(x﹣1)(x﹣2).
(4)(a+b)2(a﹣b)2.
(5)(a﹣3)(a+3)(a2+9).
(6)(m﹣2n+3)(m+2n﹣3).
(7) .
.
(8)![]() .
.
(9)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,∠ABG为锐角,AH∥BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为F(F不与A重合),若∠ECF=n°,则∠BAF的度数为_____度.(用n来表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,A(﹣2,3),B(﹣4,﹣1),C(1,0).
(1)P(x0,y0)是△ABC内任一点,经平移后对应点为P1(x0+2,y0+1),将△ABC作同样的平移,得到△A1B1C1,
①直接写出A1、B1、C1的坐标.
②若点E(a﹣2,5﹣b)是点F(2a﹣3,2b﹣5)通过平移变换得到的,求b﹣a的平方根.
(2)若Q为x轴上一点,S△BCQ=![]() S△ABC,直接写出点Q的坐标.
S△ABC,直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 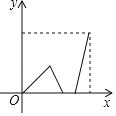
C.  D.
D. 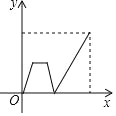
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF.

(1)你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角.
(2)试探索BE和CF有什么数量关系和位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 A(-2,0),B(0,m)两点,且线段AB= 2 ![]() ,以 AB 为边在第二象限内作正方形 ABCD。
,以 AB 为边在第二象限内作正方形 ABCD。

(1)求点 B 的坐标
(2)在 x 轴上是否存在点 Q,使△QAB 是以 AB 为腰的等腰三角形?若存在,请直接写出点 Q 的坐标,若不存在,请说明理由;
(3)如果在坐标平面内有一点 P(a,3),使得△ABP 的面积与正方形 ABCD 的面 积相等,求 a 的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com