
����Ŀ������̽����
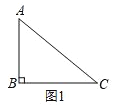
(1)��ͼ1,�ڡ�ABC��,��B=90��AB=3��BC=4������ABC�ı��ϴ��ڵ�P��ʹ��ABP����ABΪ���ĵ��������Σ���CP�ij�Ϊ______��
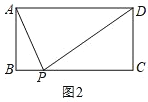
(2)��ͼ2,�ھ���ABCD��,AB=3,��BC�ϴ��ڵ�P,ʹ��APD=90�������ABCD�������Сֵ.
��������
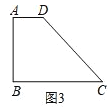
(3)��ͼ3,���ı���ABCD��,AB=3,��A=��B=90,��C=45,��CD�ϴ��ڵ�P,ʹ��APB=60�㣬�ڴ������£��ı���ABCD������Ƿ�������ֵ?�����ڣ�������ֵ���������ڣ���˵������.
���𰸡�(1) 1��![]() ��2��(2) ����ABCD�������СֵΪ18��(3)���ڣ�
��2��(2) ����ABCD�������СֵΪ18��(3)���ڣ�![]() +
+![]() .
.
����������1�����������ηֱ���⼴����
��2����ͼ2��������ADΪֱ���ġ�O��BC����ʱ���е�ΪP����ʱ��APD=90�㣬AD�ij���С�����AD�ij����ɽ��������
��3�����ڣ���ͼ3������ͼ���ȱ�������ABM�����Բ��O����ֱ��CD���O������Pʱ���ı���ABCD������������ʱ����������APB=��AMB=60������취���AD��AB���ɽ��������
��1����ͼ1������BH��AC��
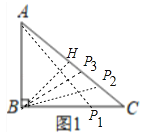
��Rt��ABC�У��ߡ�ABC=90�㣬AB=3��BC=4����AC=![]() =5��
=5��
��![]() ABBC=
ABBC=![]() ACBH����BH=
ACBH����BH=![]() ����Rt��ABH����AH=
����Rt��ABH����AH=![]() =
=![]() ��������������ۣ�
��������������ۣ�
�ٵ�BA=BP1ʱ��PC1=4��3=1��
�ڵ�BA=BP2ʱ����BH��AP2����AH=HP2=![]() ����CP2=AC��AP2=5��
����CP2=AC��AP2=5��![]() =
=![]() ��
��
�۵�AB=AP3ʱ��CP3=5��3=2��
��������������������PC��ֵΪ1��![]() ��2��
��2��
�ʴ�Ϊ��1��![]() ��2��
��2��
��2����ͼ2��������ADΪֱ���ġ�O��BC����ʱ���е�ΪP����ʱ��APD=90�㣬AD�ij���С��

����OP����OP��BC����֤�ı���BPO���ı���CDOP��������������BC=AD=6��AB=CD=3�������ABCD�������СֵΪ18��
��3�����ڣ���ͼ3������ͼ���ȱ�������ABM�����Բ��O����ֱ��CD���O������Pʱ���ı���ABCD������������ʱ����������APB=��AMB=60�㣮
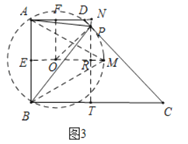
�ӳ�MO��AB��E����OF��AD��F��PT��BC��T������OP����PT��OM��R��
��AB=3��AD��BC����C=45�㣬��CD=![]() AB=3
AB=3![]() ��
��
�ߡ�ABM�ǵȱ����������ı���AEOF�Ǿ�������AE=EB=NR=RT=![]() ��AF=EO=
��AF=EO=![]() ��OM=OP=
��OM=OP=![]() ��OR=PR=
��OR=PR=![]() ����BT=AN=
����BT=AN=![]() +
+![]() ��PN=DN=TN��PT=3��
��PN=DN=TN��PT=3��![]() ��
��![]() =
=![]() ����AD=AN��DN=
����AD=AN��DN=![]() ����
����![]() ��=
��=![]() ��BC=BT+CT=
��BC=BT+CT=![]() +
+![]() +
+![]() =
=![]() ����S�ı���ABCD=
����S�ı���ABCD=![]() AB=
AB=![]() ��
��![]() ��=
��=![]() +3
+3![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ����������֧�����������������������������������Ǵ����˺ܶ������������ѧС����У�ڶ��������Ͽɵ��Ĵ����������������˵��飬���������![]() �ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��
�ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��

��1������ͼ����Ϣ���![]() =___________��
=___________��![]() =_____________��
=_____________��
��2������������ǽ�������ͳ��ͼ��ȫ��
��3�����ݳ�������Ľ���������ȫУ2000��ѧ���֣���Լ�ж��������Ͽ���������һ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���߸�AB��Ӱ�ӷֱ������˵��Ϻ�ǽ�ϣ�ͬһʱ�̣�С������1�ߵ�ֱ��MN��������Ӱ��MFΪ0.5�ף����õ��߸�AB���ڵ��ϵ�Ӱ��BD��3�ף�����ǽ�ϵ�Ӱ��CD�ĸ�Ϊ2�ף���������С������������������߸�AB�ĸ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������ڹ��������̼ۣ���������ʱ�ļ۸�ÿ��24Ԫ�����ij��˾��Ʊ1000�ɣ����������չ��в����ף��ڽ�������һ�ܽ������ڣ���������¸ù�ÿ�����̼۸����ǰһ����ǵ�������±�������λ��Ԫ��

��1������������ʱ��ÿ���Ƕ���Ԫ��
��2����֪С�����������Ʊʱ����1.5��������ѣ�����ʱ�踶�ɽ����1.5��������Ѻ�1��Ľ���˰�����������������ǰ��ȫ����Ʊ�������������������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��90��������OMƽ�֡�AOC��ONƽ�֡�BOC��

��1�������BOC��30�������MON�Ķ�����
��2�������AOB��������BOC��30���������������䣬���MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������ֵ: 2(x2y��xy)��3(x2y��xy)��4x2y������x��-1��y��![]() .
.
��2�����:��ʦ�ںڰ�����д��һ����ȷ��������̣������������ס��һ������ʽ����ʽ���£�![]() ��(��3x2��5x��7)����2x2��3x��6.������Ķ���ʽ.
��(��3x2��5x��7)����2x2��3x��6.������Ķ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ʽ����ɡ������![]() ��ֱ�ڵ���
��ֱ�ڵ���![]() ��
��![]() Ϊ�����ϵĻ������ڵ㣬ɡ��Ľ���ʾ��ͼΪ
Ϊ�����ϵĻ������ڵ㣬ɡ��Ľ���ʾ��ͼΪ![]() ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ��
��![]() ��
��![]() ��
��![]() .����
.����![]() λ�ڳ�ʼλ��
λ�ڳ�ʼλ��![]() ʱ����
ʱ����![]() ��
��![]() �غϣ�ͼ2��.��������飬��̫��������
�غϣ�ͼ2��.��������飬��̫��������![]() ��ֱʱ������Ч�����.
��ֱʱ������Ч�����.
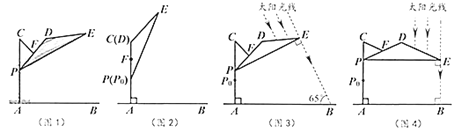
��1������10:00ʱ��̫�����������ļн�Ϊ![]() ��ͼ3����Ϊʹ����Ч����ѣ���
��ͼ3����Ϊʹ����Ч����ѣ���![]() ���
���![]() �ϵ����پ��룿�������ȷ��
�ϵ����پ��룿�������ȷ��![]() ��
��
��2������12:00ʱ��̫����������洹ֱ��ͼ4����Ϊʹ����Ч����ѣ���![]() �ڣ�1���Ļ����ϻ����ϵ����پ��룿�������ȷ��
�ڣ�1���Ļ����ϻ����ϵ����پ��룿�������ȷ��![]() ��
��
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ���κ���
Ϊ���κ���![]() ͼ��Ķ��㣬ֱ��
ͼ��Ķ��㣬ֱ��![]() �ֱ�
�ֱ�![]() �������ᣬ
�������ᣬ![]() ���ڵ�
���ڵ�![]() ��
��![]() .
.

��1���ж϶���![]() �Ƿ���ֱ��
�Ƿ���ֱ��![]() �ϣ���˵������.
�ϣ���˵������.
��2����ͼ1�������κ���ͼ��Ҳ������![]() ��
��![]() ����
����![]() ������ͼ��д��
������ͼ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��3����ͼ2����![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() �ڣ�����
�ڣ�����![]() ��
��![]() ���ڶ��κ���ͼ���ϣ��ԱȽ�
���ڶ��κ���ͼ���ϣ��ԱȽ�![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD������D��DE��AB�ڵ�E����F�ڱ�CD�ϣ�DF��BE������AF��BF.

��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF��3��BF��4��DF��5����֤��AFƽ����DAB.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com