
【题目】已知函数![]() ,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是
,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
请你根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行探究.
之间的变化规律,对该函数的图象与性质进行探究.
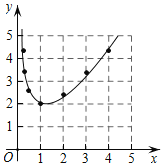
(1)如图,在平面直角坐标系![]() 中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;

(2)请根据图象写出该函数的一条性质: .
(3)当![]() 时,
时,![]() 的取值范围为 ,则
的取值范围为 ,则![]() 的取值范围为 .
的取值范围为 .
【答案】(1)画图见解析;(2)当![]() 时,y随x的增大而减小(答案不唯一,写单调性或最值中的一种都可以);(3)
时,y随x的增大而减小(答案不唯一,写单调性或最值中的一种都可以);(3)![]() ,
,![]() .
.
【解析】
(1)根据描出的点,画出该函数的图象即可;
(2)①观察图像,当![]() 时,y随x的变化而怎样变化,或②函数的最小值问题;(答案不唯一,写单调性或最值中的一种都可以)
时,y随x的变化而怎样变化,或②函数的最小值问题;(答案不唯一,写单调性或最值中的一种都可以)
(3)根据x取不同值时,y所对应的取值范围即可得到结论.
解:(1)如图所示:由光滑的曲线连接各点即可.
(2)当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
或写成:当![]() 时,函数有最小值为2.
时,函数有最小值为2.
故答案为:当![]() 时,y随x的增大而减小,(答案不唯一,写单调性或最值中的一种都可以);
时,y随x的增大而减小,(答案不唯一,写单调性或最值中的一种都可以);
(3)结合图像,当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,则
,则![]() 的取值范围为:
的取值范围为:![]() .
.
故答案为:![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( ) 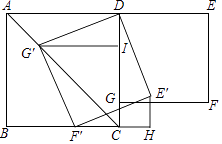
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=25°,∠ADC=115°,O为AB的中点,以点O为圆心、AO长为半径作圆,恰好点D在⊙O上,连接OD,若∠EAD=25°,下列说法中不正确的是( ) 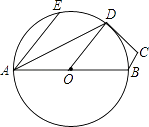
A.D是劣弧 ![]() 的中点
的中点
B.CD是⊙O的切线
C.AE∥OD
D.∠DOB=∠EAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[实际背景]预警方案确定:
设![]() ,如果当月
,如果当月![]() 则下个月要采取措施防止“猪贱伤农”.
则下个月要采取措施防止“猪贱伤农”.
[数据收集]今年2月-5月玉米、猪肉价格统计表:
月份 | 2 | 3 | 4 | 5 |
玉米价格(元/ |
|
|
|
|
猪肉价格(元/ |
|
|
|
|
[问题解决](1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等,求3月的猪肉价格![]() ;
;
(2)若今年6月及以后月份,玉米价格增长的规律不变,而每月的猪内价格按照5月的猪肉价格比上月下降的百分数继续下降,请你预测了月时是否要采取措施防止“碧败伤农”;
(3)若今年6月及以后月份,每月玉米价格增长率是当月猪肉价格增长率的![]() 倍,而每月的猪肉价格增长率都为
倍,而每月的猪肉价格增长率都为![]() .则到7月时只用
.则到7月时只用![]() 元就可以买到
元就可以买到![]() 克猪肉和
克猪肉和![]() 克玉米.请你预测8月时是否要采取措施防止“猪贱伤衣”.
克玉米.请你预测8月时是否要采取措施防止“猪贱伤衣”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,M![]() 表示a,b,c这三个数的平均数,min
表示a,b,c这三个数的平均数,min![]() 表示a,b,c这三个数中最小的数,如:
表示a,b,c这三个数中最小的数,如:
M![]() ,min
,min![]() =-1;
=-1;
M![]() ,min
,min![]() =
=![]() ;
;
解决下列问题:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min![]() =2,则x的取值范围是______________;
=2,则x的取值范围是______________;
(3) ①若M![]() =min
=min![]() ,那么x=______________;
,那么x=______________;
②根据①,你发现结论“若M![]() =min
=min![]() ,则______________;(填a,b,c的大小关系);
,则______________;(填a,b,c的大小关系);
③运用②解决问题:(写出求解的过程)
若M![]() =min
=min![]() ,
,
求x+y 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成,若完成该工程甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com