
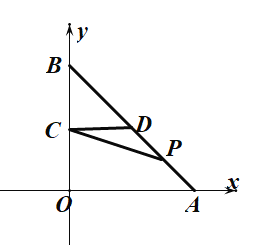
【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,
为坐标原点,![]() 轴上点
轴上点![]() 的横坐标为
的横坐标为![]() ,
,![]() 轴上点
轴上点![]() 的纵坐标为
的纵坐标为![]() ,且
,且![]() ,过
,过![]() 中点
中点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]()
(1)求点![]() 的坐标;
的坐标;
(2)第一象限的点![]() 在
在![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() (
(![]() ),用含
),用含![]() 的式子表示
的式子表示![]() ,并直接写出相应的
,并直接写出相应的![]() 的范围;
的范围;
(3)在(2)的条件下,过点![]() 作直线
作直线![]() 的垂线,点
的垂线,点![]() 为垂足,
为垂足,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,若
,若![]() ,求
,求![]() 值.
值.

【答案】(1)![]() ;(2)
;(2)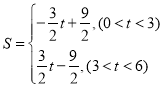 ;(3)
;(3)![]()
【解析】
(1)先对原式进行整理,根据二次根式与平方的非负性求出a,b的值,再利用三角形中位线的性质即可求出D的横纵坐标;
(2)先用待定系数法求出直线AB的解析式,然后分两种情况:P点在直线CD的上方和下方,利用三角形的面积公式即可表示出S与t之间的关系式;
(3)过点![]() 作
作![]() 的垂线,点
的垂线,点![]() 为垂足,
为垂足,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的垂线,点T为垂足,先证明
的垂线,点T为垂足,先证明![]() 得出
得出![]() ,然后利用角平分线的性质和等腰直角三角形的性质证明
,然后利用角平分线的性质和等腰直角三角形的性质证明![]() ,则有
,则有![]() ,
,![]() ,进而得出
,进而得出![]() ,接着证明
,接着证明![]() 得出
得出![]() ,
,![]() ,进而有
,进而有![]() ,最后分别用含t的代数式表示出
,最后分别用含t的代数式表示出![]() 和
和![]() ,求出t的值,则
,求出t的值,则![]() 可求.
可求.
(1)解:∵![]()
即![]()
∴![]()
∴![]()
∵CD是![]() 的中位线
的中位线
∴![]()
∴![]()
(2)设直线AB的解析式为![]()
将点代入解析式中得
![]() 解得
解得![]()
∴直线AB的解析式为![]()
当![]() 时,
时,![]()
设底边CD上的高为h,
当![]() 时,
时,

![]()
∴![]() (
(![]() )
)
当![]() 时,
时,
![]()
∴![]() (
(![]() )
)
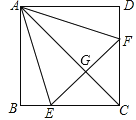
综上所述,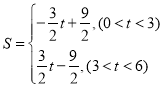
(3)过点![]() 作
作![]() 的垂线,点
的垂线,点![]() 为垂足,
为垂足,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的垂线,点T为垂足.
的垂线,点T为垂足.

∵![]()
∴![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]()
即![]()
∴![]()
∵![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
∴![]()
![]()
∴![]()
∴![]()
∵![]()
∴![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
∴![]()
![]()
![]()
∴![]()
∴![]()
解得![]()
∴![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,OD,连接CO并延长交AD于点M.则下列结论中:
①FG=2AO;②OD∥HE;③![]() ;④2OE2=AHDE;⑤GO+BH=HC
;④2OE2=AHDE;⑤GO+BH=HC
正确结论的个数有( )
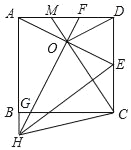
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
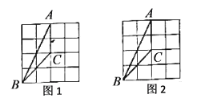
【题目】顶点都在格点上的的三角形叫做格点三角形,如图,在![]() 的方格纸中,
的方格纸中,![]() 是格点三角形.
是格点三角形.
(1)在图![]() 中,以点
中,以点![]() 为对称中心,作出一个与
为对称中心,作出一个与![]() 成中心对称的格点三角形
成中心对称的格点三角形![]() ,并在题后横线上直接写出
,并在题后横线上直接写出![]() 与
与![]() 的位置关系: .
的位置关系: .
(2)在图![]() 中,以
中,以![]() 所在的直线为对称轴,作出一个与
所在的直线为对称轴,作出一个与![]() 成轴对称的格点三角形
成轴对称的格点三角形![]() ,并在题后横线上直接写出
,并在题后横线上直接写出![]() 是什么形状的特殊三角形: .
是什么形状的特殊三角形: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
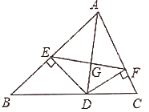
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的高,连接
的高,连接![]() 交
交![]() 于
于![]() .下列结论:①
.下列结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() 平分
平分![]() ;④当
;④当![]() 为
为![]() 时,
时,![]() ,其中不正确的结论的个数为( )
,其中不正确的结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读思考)阅读下列材料:
已知“x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,
∴x=y+2
又∵x>1
∴y+2>1
∴y>﹣1
又∵y<0
∴﹣1<y<0 ①
同理1<x <2 ②
由①+②得﹣1+1<x+y<0+2
∴x+y 的取值范围是0<x+y <2
(启发应用)请按照上述方法,完成下列问题:
已知x ﹣y =3,且x > 2,y <1,则x+y的取值范围是 ;
(拓展推广)请按照上述方法,完成下列问题:
已知x+y=2,且x>1,y>﹣4,试确定x﹣y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com