
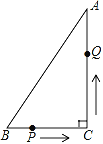
【题目】如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当t为何值时,P、Q两点的距离为5![]() cm?
cm?
(2)当t为何值时,△PCQ的面积为15cm2?
(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
【答案】(1)t=1;(2)经过2或1.5s后,S△PCQ的面积为15cm2;(3)当点P运动1.75秒时,四边形BPQA的面积最小为: ![]() cm2.
cm2.
【解析】(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为![]() cm2;
cm2;
(2)根据三角形的面积公式![]() 便可求出经过2或1.5s后,S△PCQ的面积为15 cm2;
便可求出经过2或1.5s后,S△PCQ的面积为15 cm2;
(3)根据三角形的面积公式![]() 以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
解:(1)∵在Rt△ABC中,AC=24cm,BC=7cm,
∴AB=25cm,
设经过ts后,P、Q两点的距离为5![]() cm,
cm,
ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5![]() )2;
)2;
解得t=1或t=-![]() (不合题意舍去);
(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=![]() =
=![]() ×(7-2t)×5t=15
×(7-2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=![]() ×PC×CQ=
×PC×CQ=![]() ×(7-2t)×5t=
×(7-2t)×5t=![]() ×(-2t2+7t)
×(-2t2+7t)
当t=-![]() 时,即t=
时,即t=![]() =1.75s时,△PCQ的面积最大,
=1.75s时,△PCQ的面积最大,
即S△PCQ=![]() ×PC×CQ=
×PC×CQ=![]() ×(7-2×1.75)×5×1.752=
×(7-2×1.75)×5×1.752=![]() (cm2),
(cm2),
∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大=![]() ×7×24-
×7×24-![]() =
=![]() (cm2),
(cm2),
当点P运动1.75秒时,四边形BPQA的面积最小为: ![]() cm2.
cm2.


科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的解题过程的横线上填空,并在括号内注明理由。
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴DF∥AC(_____________________)
∴∠D=_____(______________________)
∵∠C=∠D(已知)
∴∠1=_____(___________________)
∴BD∥CE(_______________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 分别为
分别为![]() 边上的动点.
边上的动点.
(1)若点![]() 分别为
分别为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)若![]() ,
,
①求证: ![]() ∽
∽![]() ;
;
②试问![]() 与
与![]() 相似吗?并说明理由.
相似吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润为1950万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
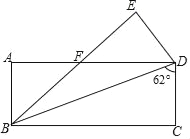
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
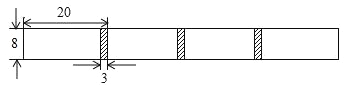
![]() 根据题意,将下面的表格补充完整:
根据题意,将下面的表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | 5 |
|
纸条长度 | 20 | ______ | 54 | 71 | ______ |
|
![]() 直接写出用x表示y的关系式:______ ;
直接写出用x表示y的关系式:______ ;
![]() 要使粘合后的总长度为1006cm,需用多少张这样的白纸?
要使粘合后的总长度为1006cm,需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
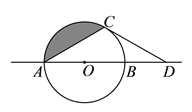
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,
的直径, ![]() 是⊙
是⊙![]() 上一点,连接
上一点,连接![]() ,⊙
,⊙![]() 外的一点
外的一点![]() 在直线
在直线![]() 上.
上.
(![]() )若
)若![]() ,
, ![]() .
.
①求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
②阴影部分的面积是__________.(结果保留![]() )
)
(![]() )当点
)当点![]() 在⊙
在⊙![]() 上运动时,若
上运动时,若![]() 是⊙
是⊙![]() 的切线,探究
的切线,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com