
【题目】如图,数轴上有A、B、C三点,点A和点B所表示的数分别为﹣3和+![]() ,点C到点A、点B的距离相等.
,点C到点A、点B的距离相等.
![]()
(1)点C表示的数为 ;
(2)若数轴上有一点P,若满足PA+PB=10,求点P表示的数;
(3)若数轴上有一点Q.若满足QA+QB﹣QC=![]() ,求点Q表示的数.
,求点Q表示的数.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或﹣
或﹣![]() 或
或![]() .
.
【解析】
(1)先根据数轴上两点的距离![]() 较大的数
较大的数![]() 较小的数计算
较小的数计算![]() 的长,由点
的长,由点![]() 到点
到点![]() 、点
、点![]() 的距离相等,可得结论;
的距离相等,可得结论;
(2)设点![]() 表示的数是
表示的数是![]() ,分两种情况:根据
,分两种情况:根据![]() 列方程可得结论;
列方程可得结论;
(3)设点![]() 表示的数为
表示的数为![]() ,分四种情况:根据
,分四种情况:根据![]() 列方程可得结论.
列方程可得结论.
解:(1)![]() 点
点![]() 和点
和点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 表示的数为
表示的数为![]() ,
,
故答案为:![]() ;
;
(2)设点![]() 表示的数是
表示的数是![]() ,
,
![]() ,
,
分两种情况:
①![]() 在
在![]() 的左边时,
的左边时,![]() ,
,![]()
②![]() 在
在![]() 的右边时,
的右边时,![]() ,
,![]()
![]() 点
点![]() 表示的数是
表示的数是![]() 或
或![]() ;
;
(3)设点![]() 表示的数为
表示的数为![]() ,
,
分四种情况:
①当![]() 在点
在点![]() 的左边时,如图1,
的左边时,如图1,
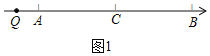
![]() ,
,
![]() ,即
,即![]() ,
,![]()
![]() 点
点![]() 表示的数是
表示的数是![]() ;
;
②当![]() 在点
在点![]() 的右边时,如图2,
的右边时,如图2,
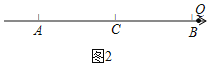
![]() ,
,
![]() ,即
,即![]() ,
,![]()
![]() 点
点![]() 表示的数是
表示的数是![]() ;
;
③当![]() 在点
在点![]() 和点
和点![]() 之间时,如图3,
之间时,如图3,
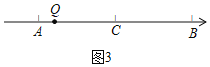
![]() ,
,
![]() ,即
,即![]() ,
,![]()
![]() 点
点![]() 表示的数是
表示的数是![]() ;
;
④当![]() 在点
在点![]() 和点
和点![]() 之间时,如图4,
之间时,如图4,
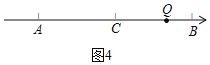
![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
![]() 点
点![]() 表示的数是
表示的数是![]() ;
;
综上,点![]() 表示的数是
表示的数是![]() 或
或![]() 或
或![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元。
(1)求每个甲种规格的排球和每个已汇总规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
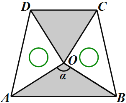
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
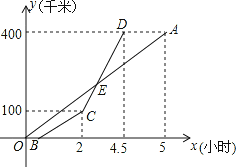
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
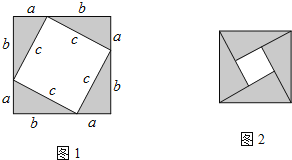
【题目】阅读下面的材料:勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述方法证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
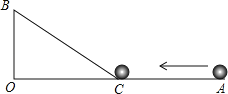
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
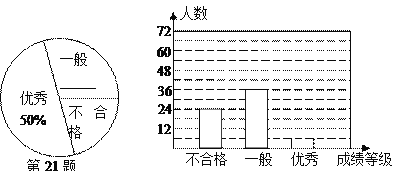
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com