
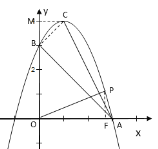
【题目】在平面直角坐标系xOy中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,其顶点为C.
,其顶点为C.

(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n,m)的点叫做坐标为(m,n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
【答案】(1)![]() ,顶点C的坐标为:(1,4);(2)点M的坐标为(
,顶点C的坐标为:(1,4);(2)点M的坐标为(![]() ,1)或(
,1)或(![]() ,1);(3)点P的坐标为(
,1);(3)点P的坐标为(![]() ,
,![]() ).
).
【解析】
(1)将点![]() 和
和![]() 代入
代入![]() 即可求出;
即可求出;
(2)设点M的坐标为(n,m),则其反射点的坐标为(m,n),根据点M的反射点在抛物线的对称轴上得到m=1,即M(n,1),将点M坐标代入解析式求出n即可得到坐标;
(3)根据点![]() 和
和![]() 求出AB=
求出AB=![]() ,过点C作CM⊥y轴与M,根据C(1,4),求出CM=BM=1,推出∠ABC=90°,
,过点C作CM⊥y轴与M,根据C(1,4),求出CM=BM=1,推出∠ABC=90°,![]() ,设点P的坐标为(x,
,设点P的坐标为(x,![]() ),过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,证明△POF∽△CAB,列关系式求出x即可得到点P的坐标.
),过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,证明△POF∽△CAB,列关系式求出x即可得到点P的坐标.
(1)将点![]() 和
和![]() 代入
代入![]() 得
得
![]() ,解得
,解得![]() ,
,
∴![]() =
=![]() ,
,
∴顶点C的坐标为:(1,4);
(2)设点M的坐标为(n,m),则其反射点的坐标为(m,n),
∵点M的反射点在抛物线的对称轴上,
∴m=1,即M(n,1),
代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
∴点M的坐标为(![]() ,1)或(
,1)或(![]() ,1);
,1);
(3)∵点![]() 和
和![]() ,
,
∴OA=OB=3,
∴AB=![]() ,
,
∴∠ABO=∠BAO=45°,
过点C作CM⊥y轴与M,
∵C(1,4),
∴CM=BM=1,
∴∠CBM=∠BCM=45°,
∴∠ABC=90°,
∴![]() ,
,
设点P的坐标为(x,![]() ),
),
过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,
∵∠POA=∠ACB,
∴△POF∽△CAB,
∴![]() ,
,
∴![]() ,
,
解得x=![]() 或x=
或x=![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() =
=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】赣南脐橙果大形正,肉质脆嫩,风味浓甜芳香,深受大家的喜爱.某脐橙生产基地生产的礼品盒包装的脐橙每箱的成本为30元,按定价50元出售,每天可销售200箱.为了增加销量,该生产基地决定采取降价措施,经市场调研,每降价1元,日销售量可增加20箱.


(1)求出每天销售量y(箱)与销售单价x(元)之间的函数关系式;
(2)若该生产基地每天要实现最大销售利润,每箱礼品盒包装的脐橙应定价多少元?每天可实现的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
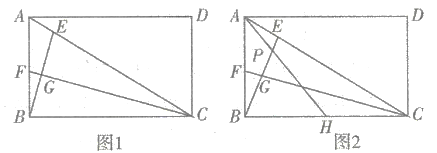
【题目】如图,在矩形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一动点,连接
上一动点,连接![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() 于点
于点 ![]() .
.
(1)如图1,若![]() 恰好平分
恰好平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于点
于点 ![]() .
.
求证:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
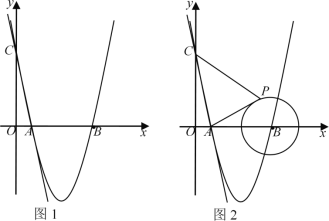
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
(1)求抛物线的解析式及![]() 点坐标;
点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若![]() 点是半径为2的⊙
点是半径为2的⊙![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最小为_________.(直接写出结果)
的值最小为_________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
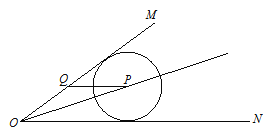
A.4<r<12B.2<r<12C.4<r<8D.r>4
查看答案和解析>>
科目:初中数学 来源: 题型:
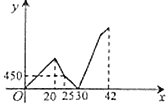
【题目】小杰早上从家匀速步行去学校,走到途中发现英语书忘在家里了,随即打电话给爸爸,爸爸立即送英语书去,小杰掉头以原速往回走,几分钟后,路过一家文具店,此时还未遇到爸爸,小杰便在文具店购买了几个笔记本,刚付完款,爸爸刚好赶到,将英语书交给了小杰(途中小杰打电话、小杰的爸爸找英语书的时间忽略不计):然后,爸爸原速返回,同时小杰把速度提高到原来的![]() 前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离
前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离![]() (米)与小杰从家出发的时间
(米)与小杰从家出发的时间![]() (分钟)的函数关系如图所示,则家与学校相距______米.
(分钟)的函数关系如图所示,则家与学校相距______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
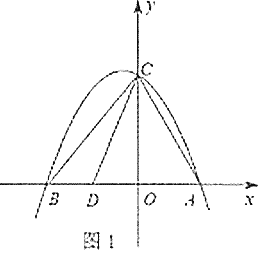
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,且点
,且点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() .
.
(1)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一动点,在线段
上方抛物线上的一动点,在线段![]() 上有一动点
上有一动点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
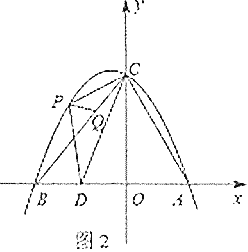
(2)将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,设旋转中的直线
旋转,设旋转中的直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的进水量与出水量分别是( )
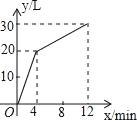
A.5L,3.75LB.2.5L,5LC.5L,2.5LD.3.75L,5L
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com