
����Ŀ����֪����x��һԪ���η���mx2+��3m+1��x+3=0�� 
��1����֤���÷���������ʵ������
��2�����������y=mx2+��3m+1��x+3��x�ύ��A��B���������㣨��A�ڵ�B��ࣩ����mΪ����������������ߵı���ʽ��
��3���ڣ�2���������£�������y=mx2+��3m+1��x+3��y�ύ�ڵ�C����B����y��ĶԳƵ�ΪD������������ک�3��x�ܩ� ![]() ֮��IJ���Ϊͼ��G�����ͼ��G����ƽ��n��n��0������λ���Ⱥ���ֱ��CD�й����㣬��n��ȡֵ��Χ��
֮��IJ���Ϊͼ��G�����ͼ��G����ƽ��n��n��0������λ���Ⱥ���ֱ��CD�й����㣬��n��ȡֵ��Χ��
���𰸡�
��1��֤�����ɸ����б�ʽ���ɵã���=��3m+1��2��4��m��3=��3m��1��2��
�ߣ�3m��1��2��0��
�����0��
��ԭ����������ʵ����
��2���⣺��y=0����ômx2+��3m+1��x+3=0��
��ã�x1=��3��x2=�� ![]() ��
��
����������x����������ĺ������Ϊ��������mΪ��������
��m=1��
�������ߵĽ���ʽΪ��y=x2+4x+3
��3���⣺��ͼ��
�ߵ�x=0ʱ��y=3��
��C��0��3����
�ߵ�y=0ʱ��x1=��3��x2=��1��
�֡ߵ�A�ڵ�B����࣬
��A����3��0����B����1��0����
�ߵ�D���B����y��Գƣ�
��D��1��0����
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
�� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��CD�ı���ʽΪ��y=��3x+3��
�֡ߵ�x=�� ![]() ʱ��y=
ʱ��y= ![]() ��
��
���E���� ![]() ��
�� ![]() ����
����
��ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨��3+n��0����E�䣨�� ![]() +n��
+n�� ![]() ����
����
��ֱ��y=��3x+3������A�䣨��3+n��0��ʱ���ã���3����3+n��+3=0����ã�n=4��
��ֱ��y=��3x+3������E�䣨�� ![]() +n��
+n�� ![]() ����ʱ���ã���3����
����ʱ���ã���3���� ![]() +n��+3=
+n��+3= ![]() ����ã�n=
����ã�n= ![]() ��
��
��n��ȡֵ��Χ�� ![]() ��n��4��
��n��4��
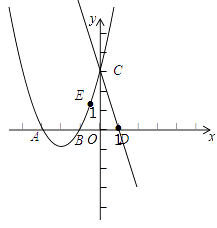
����������1������������б�ʽ�����жϡ���ȡֵ��Χ�����ɵ�֤����2�����������ʽ��ʾ�������������⣬���m��ֵ���ɵ������ߵĽ���ʽ����3���������A��B��C��D�����꣬���ݴ���ϵ�������ֱ��CD�Ľ���ʽ����ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨��3+n��0����E�䣨�� ![]() +n��
+n�� ![]() �������ݵ���ֱ���ϣ����ȡֵ��Χ���ɣ�
�������ݵ���ֱ���ϣ����ȡֵ��Χ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��������ABC�У���ACB��90�㣬��A��33�㣬��������ABC��AB��������ƽ�Ƶõ�������DEF.
(1)�������E�Ķ�����
(2)��AE��9 cm��DB��2 cm�����BE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��E��F��C��һ��ֱ���ϣ�AE��CF����E��F�ֱ���DE��AC��BF��AC����AB��CD����֤��BDƽ��EF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��AB���е㣬��F��BC�ӳ�����һ�㣬����DF����AC�ڵ�E������BE����A=��ABE��
��1����֤��DF���߶�AB�Ĵ�ֱƽ���ߣ�
��2����AB=AC����A=46��ʱ�����EBC����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
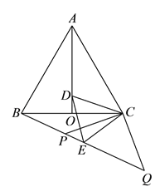
����Ŀ����ͼ���ȱ���ABC�У� AO����BAC�Ľ�ƽ���ߣ� DΪ AO��һ�㣬�� CDΪһ������ CD�·����ȱ���CDE������BE��
��1����֤����ACD�ա�BCE��
��2���ӳ�BE��Q�� PΪBQ��һ�㣬���� CP��CQʹ CP=CQ=5���� BC=6����PQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
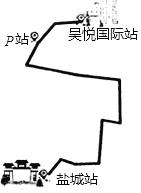
����Ŀ������ÿ�����һ�Ρ�һ��ţ�̵ı��ߡ��������ò��еķ�ʽļ���ƿ������ս��·�ߡ���������ͳ�վ�������Ź涨����·�����յ����ù���վ���ס���������������ͬʱ��������֪������ٶ�Ϊ6km/h��������ٶ�Ϊ5km/h�������鵽���յ��������3km/h���ٶȰ�ԭ��·���أ�����;�е�Pվ������������Pվ�����ù���վ֮���·��Ϊ1.5km
��1������ս��·�ߡ����ܳ���
��2�������鵽���յ�ʱ���������յ㻹�ж���·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����仭ͼ����ͼ��ֱ��CD��ֱ��AB�ཻ��C��
����������仭ͼ��
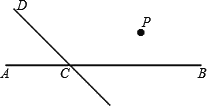
��1������P��PQ��CD����AB�ڵ�Q��
��2������P��PR��CD������ΪR��
��3������DCB=120�㣬�����PQC�Ƕ��ٶȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ҿ���ѧУ8ǧ�ף�һ���糿С���ﳵ��ѧ��;��ǡ����������������ʮ��·�ڴ���С���ѹ���·��С��ͣ�³�Э���������壬�����Ӻ�Ϊ�˲��ٵ������ӿ����ﳵ��У���ٶȣ���У��С��������ξ��������˹���ͼ����ͼ����ͼ�������С�����е�·��![]() ��ǧ�ף��������õ�ʱ��
��ǧ�ף��������õ�ʱ��![]() �����ӣ�֮��Ĺ�ϵ�������ͼ����������⣺
�����ӣ�֮��Ĺ�ϵ�������ͼ����������⣺
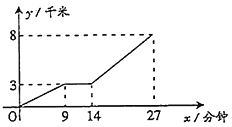
��1��С���ﳵ��ʻ�˶���ǧ��ʱ��Э���������壿Э�������������˼����ӣ�
��2��С���Ӽҳ�����ѧУ�����˶���ʱ�䣿
��3�����û��Э���������壬�Ա��ֳ���ʱ���ٶ���ʻ����ô����ʵ������絽������ѧУ���ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ����һ��![]() Ϊ�˵�������
Ϊ�˵�������![]() ��ʹ
��ʹ![]() ����һ��ֱ�����ǰ�
����һ��ֱ�����ǰ�![]() ������
������![]() ����ֱ�Ƕ�����ڵ�
����ֱ�Ƕ�����ڵ�![]() ����
����
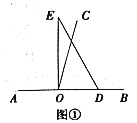
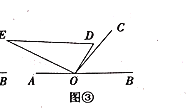
��1����ͼ�٣���ֱ�����ǰ�![]() ��һ��
��һ��![]() ��������
��������![]() �ϣ���
�ϣ���![]() ____
____![]() ��
��
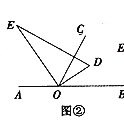
��2����ͼ������ֱ�����ǰ�![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת����ij��λ�ã���
��ʱ��ת����ij��λ�ã���![]() ǡ��ƽ��
ǡ��ƽ��![]() ����
����![]() ���ڵ������Ƿ�Ϊ
���ڵ������Ƿ�Ϊ![]() ��ƽ���ߣ���˵�����ɣ�
��ƽ���ߣ���˵�����ɣ�
��3����ͼ�ۣ�����![]() �ǵ�ֱ�����ǰ�
�ǵ�ֱ�����ǰ�![]() ��ͼ�ٵ�λ�ÿ�ʼ�Ƶ�
��ͼ�ٵ�λ�ÿ�ʼ�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ���ʱ����ת������ת��Ϊ
���ٶ���ʱ����ת������ת��Ϊ![]() ����ת��ʱ��Ϊ
����ת��ʱ��Ϊ![]() �룬����ת�������Ƿ�������ǰ��һ������
�룬����ת�������Ƿ�������ǰ��һ������![]() ��ֱ�������ڣ���ֱ��д����ʱ
��ֱ�������ڣ���ֱ��д����ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com