
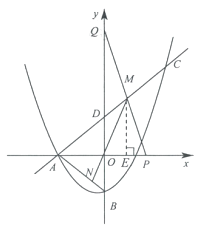
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
【答案】
(1)
解:把点C(6,![]() )代入抛物线得:
)代入抛物线得:![]() =9+
=9+![]() +c.
+c.
解得c=-3.
当y=0时,![]() x2+
x2+![]() x-3=0.
x-3=0.
解得:x1=-4,x2=3.
∴A(-4,0).
设直线AC的函数表达式为:y=kx+b(k≠0).
把A(-4,0),C(6,![]() )代入得:
)代入得:
![]()
解得:![]()
∴直线AC的函数表达式为:y=![]() x+3.
x+3.
(2)
①证明:∵在Rt△AOB中,tan∠OAB=![]() =
=![]() .
.
在Rt△AOB中,tan∠OAD=![]() =
=![]() .
.
∴∠OAB=∠OAD.
∵在Rt△POQ中,M为PQ中点.
∴OM=MP.
∴∠MOP=∠MPO.
又 ∵∠MOP=∠AON.
∴∠APM=∠AON.
∴△APM∽△AON.
②解:如下图,过点M作ME⊥x轴于点E.
∵OM=MP.
∴OE=EP.
又∵点M的横坐标为m.
∴AE=m+4,AP=2m+4.
∵tan∠OAD=![]() .
.
∴cos∠EAM=cos∠OAD=![]() .
.
∴AM=![]() AE=
AE=![]() .
.
∵△APM∽△AON.
∴![]() =
=![]() .
.
∴AN=![]() =
=![]() .
.
【解析】(1)把点C(6,![]() )代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
)代入抛物线求出c的值,令y=0求出A点坐标,再用待定系数法求出直线AC的函数表达式.
(2)①在Rt△AOB中,tan∠OAB=![]() =
=![]() . 在Rt△AOB中,tan∠OAD=
. 在Rt△AOB中,tan∠OAD=![]() =
=![]() .从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
.从而得出∠OAB=∠OAD;在Rt△POQ中,M为PQ中点得出OM=MP.∠APM=∠AON;从而证明△APM∽△AON.
②如上图,过点M作ME⊥x轴于点E;由OM=MP.得出OE=EP;点M的横坐标为m;得出AE=m+4,AP=2m+4.
根据tan∠OAD=![]() .求出cos∠EAM=cos∠OAD=
.求出cos∠EAM=cos∠OAD=![]() ;再根据△APM∽△AON;得出AN=
;再根据△APM∽△AON;得出AN=![]() =
=![]() .
.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 ![]() 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 ![]() 的值为 .
的值为 . 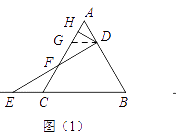
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值.
的值.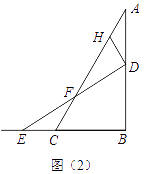
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 ![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).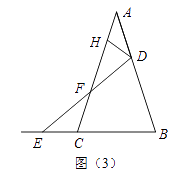
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班长调查了三班近 10 天的数学课堂小测验,在这 10 天,小测验的不及格人数为(单位:个)0,2,0, 3,1,1,0,2,5,1.在这 10 天中小测验不及格的人数( )
A. 中位数为 1.5 B. 方差为 1.5 C. 极差为 1.5 D. 标准差为 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .

查看答案和解析>>
科目:初中数学 来源: 题型:
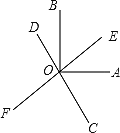
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.过点
的中点.过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() .将
.将 ![]() 沿点
沿点 ![]() 到点
到点 ![]() 的方向平移,得到
的方向平移,得到 ![]() .设
.设 ![]() 、
、 ![]() 分别是
分别是 ![]() 、
、 ![]() 的中点,当点
的中点,当点 ![]() 与点
与点 ![]() 重合时,四边形
重合时,四边形 ![]() 的面积为( )
的面积为( )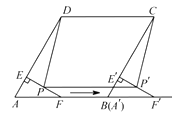
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
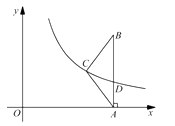
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
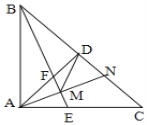
【题目】如图,等腰![]() 中,
中,![]() =90°,
=90°,![]() 于
于![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() ;上述结论中正确的个数是( )
;上述结论中正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
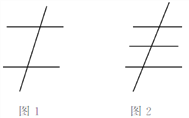
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com