【答案】
分析:(1)利用待定系数法求出抛物线的解析式;
(2)关键是求出△ACP面积的表达式,然后利用二次函数求极值的方法,求出△ACP面积的最大值;
(3)如图(3)所示,以BC为边,在线段BC两侧分别作正方形,正方形的其他四个顶点均可以使得“△BCQ是以BC为腰的等腰直角三角形”,因此有四个点符合题意要求;
(4)如图(4)所示,若以点B、Q、E为顶点的三角形与△AOC相似,有两种情况,需要分类讨论,不要漏解;
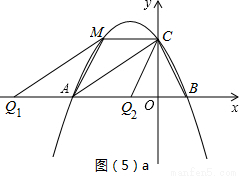
(5)以A、C、M、Q为顶点的四边形是平行四边形,有四种情况,分别如图(5)a、图(5)b所示,注意不要漏解.
解答:解:(1)由抛物线y=ax
2+bx+2过点A(-3,0),B(1,0),则
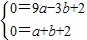
解这个方程组,得a=-

,b=-

.
∴二次函数的关系解析式为y=-

x
2-

x+2.
(2)设点P坐标为(m,n),则n=-

m
2-

m+2.
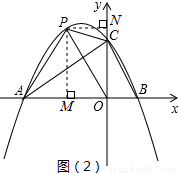
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM=-

m
2-

m+2,PN=-m,AO=3.
当x=0时,y=-

×0-

×0+2=2,所以OC=2
S
△PAC=S
△PAO+S
△PCO-S
△ACO
=

AO•PM+

CO•PN-

AO•CO
=

×3•(-

m
2-

m+2)+

×2•(-m)-

×3×2
=-m
2-3m
∵a=-1<0
∴函数S
△PAC=-m
2-3m有最大值
当m=-

=-

时,S
△PAC有最大值.
此时n=-

m
2-

m+2=-

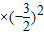
-
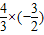
+2=

∴存在点P(-

,

),使△PAC的面积最大.
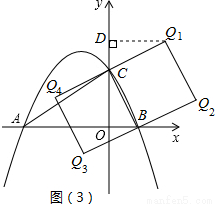
(3)如图(3)所示,以BC为边在两侧作正方形BCQ
1Q
2、正方形BCQ
4Q
3,则点Q
1,Q
2,Q
3,Q
4为符合题意要求的点.
过Q
1点作Q
1D⊥y轴于点D,易证△Q
1CD≌△CBO,
∴Q
1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q
1(2,3);
同理求得Q
2(3,1),Q
3(-1,-1),Q
4(-2,1).
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q
1(2,3),Q
2(3,1),Q
3(-1,-1),Q
4(-2,1).
(4)如图(4)所示,设E(n,0),则BE=1-n,QE=-

n
2-

n+2.
假设以点B、Q、E为顶点的三角形与△AOC相似,则有两种情况:
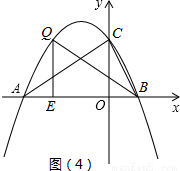
①若△AOC∽△BEQ,则有:
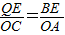
,
即
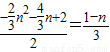
,化简得:n
2+n-2=0,
解得n
1=-2,n
2=1(与B重合,舍去),∴n=-2,QE=-

n
2-

n+2=2.
∴Q(-2,2);
②若△AOC∽△BQE,则有:
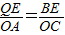
,
即
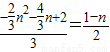
,化简得:4n
2-n-3=0,
解得n
1=-

,n
2=1(与B重合,舍去),∴n=-

,QE=-

n
2-

n+2=
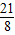
.
∴Q(-

,
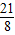
).
综上所述,存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似.
Q点坐标为(-2,2)或(-

,
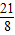
).
(5)假设存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.
①若CM平行于x轴,如图(5)a所示,有符合要求的两个点Q
1,Q
2,此时Q
1A=Q
2A=CM.
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=-1对称,
∴M(-2,2),∴CM=2.
由Q
1A=Q
2A=CM=2,得到Q
1(-5,0),Q
2(-1,0);
②若CM不平行于x轴,如图(5)b所示.过点M作MG⊥x轴于G,
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即y
M=-2.
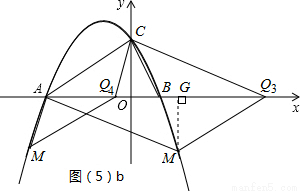
设M(x,-2),则有-

x
2-

x+2=-2,解得x=-1±
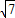
.
又QG=3,∴x
Q=x
G+3=2±
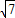
,
∴Q
3(2+
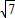
,0),Q
4(2-
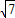
,0).
综上所述,存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.Q点坐标为:Q
1(-5,0),Q
2(-1,0),Q
3(2+
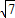
,0),Q
4(2-
,0).
注:解答中给出(3)(4)(5)问解题过程,只是为了同学们易于理解,原题并未要求.
点评:本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、二次函数极值、全等三角形、相似三角形、正方形、等腰直角三角形等重要知识点,难度较大,对考生能力要求较高.本题核心是存在性问题,第(3)(4)(5)问均涉及点的存在性,注意认真分析,在多种情况时需要分类讨论;另外注意求点坐标的方法,全等三角形与相似三角形在其中发挥重要作用,需要认真体会.

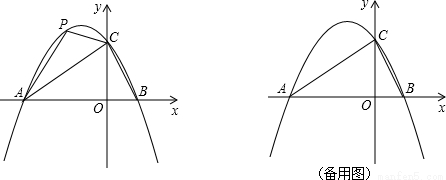
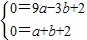
 ,b=-
,b=- .
. x2-
x2- x+2.
x+2. m2-
m2- m+2.
m+2.
 m2-
m2- m+2,PN=-m,AO=3.
m+2,PN=-m,AO=3. ×0-
×0- ×0+2=2,所以OC=2
×0+2=2,所以OC=2 AO•PM+
AO•PM+ CO•PN-
CO•PN- AO•CO
AO•CO ×3•(-
×3•(- m2-
m2- m+2)+
m+2)+ ×2•(-m)-
×2•(-m)- ×3×2
×3×2 =-
=- 时,S△PAC有最大值.
时,S△PAC有最大值. m2-
m2- m+2=-
m+2=-
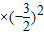 -
-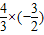 +2=
+2=
 ,
, ),使△PAC的面积最大.
),使△PAC的面积最大.
 n2-
n2- n+2.
n+2.
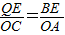 ,
,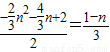 ,化简得:n2+n-2=0,
,化简得:n2+n-2=0, n2-
n2- n+2=2.
n+2=2.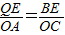 ,
,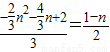 ,化简得:4n2-n-3=0,
,化简得:4n2-n-3=0, ,n2=1(与B重合,舍去),∴n=-
,n2=1(与B重合,舍去),∴n=- ,QE=-
,QE=- n2-
n2- n+2=
n+2=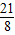 .
. ,
,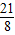 ).
).
 ,
,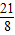 ).
).
 x2-
x2- x+2=-2,解得x=-1±
x+2=-2,解得x=-1±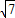 .
.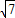 ,
,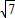 ,0),Q4(2-
,0),Q4(2-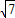 ,0).
,0).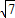 ,0),Q4(2-
,0),Q4(2-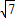 ,0).
,0).

 阅读快车系列答案
阅读快车系列答案 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.