
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.
首先,确定自变量![]() 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被![]() 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着![]() 值的减小,
值的减小,![]() 的值会越来越大…,由此,可以大致画出
的值会越来越大…,由此,可以大致画出![]() 在
在![]() 时的部分图象,如图所示:
时的部分图象,如图所示:
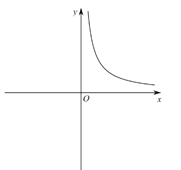
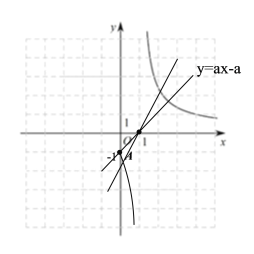
利用同样的方法,我们可以研究函数![]() 的图象与性质.通过分析解析式画出部分函数图象如图所示.
的图象与性质.通过分析解析式画出部分函数图象如图所示.
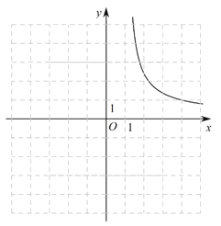
(1)请沿此思路在图中完善函数图象的草图并标出此函数图象上横坐标为0的点![]() ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)
(2)观察图象,写出该函数的一条性质:__________;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数![]() 的取值范围: __________.
的取值范围: __________.
【答案】(1)见解析;(2)当![]() 时,
时,![]() 随
随![]() 增大而减小;(3)
增大而减小;(3)![]()
【解析】
(1)先得出函数![]() 自变量
自变量![]() 的取值范围,再分析解析式,得到
的取值范围,再分析解析式,得到![]() 随
随![]() 的变化趋势,由此完善函数图象即可;令
的变化趋势,由此完善函数图象即可;令![]() 求出y的值即可得出点A坐标;
求出y的值即可得出点A坐标;
(2)根据函数图象得出其增减性即可;
(3)将所求问题看成函数![]() 与一次函数
与一次函数![]() 的交点问题,先找出一个临界位置,再根据一次函数的性质即可得.
的交点问题,先找出一个临界位置,再根据一次函数的性质即可得.
(1)由二次根式的被开方数的非负性、分式的分母不能为0得: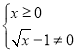
解得:![]() 且
且![]()
令![]() 得
得![]()
则点A坐标为![]()
分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值会越来越小;当
的值会越来越小;当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值会减小,且逐渐接近于零,由此,完善函数图象如图所示:
的值会减小,且逐渐接近于零,由此,完善函数图象如图所示:
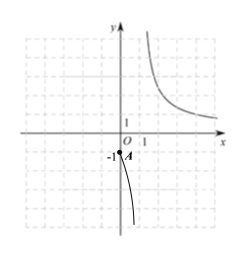
(2)由(1)图象可知,当![]() 时,
时,![]() 随
随![]() 增大而减小;(注:答案不唯一)
增大而减小;(注:答案不唯一)
(3)由题意得,函数![]() 与一次函数
与一次函数![]() 有两个交点
有两个交点
一次函数![]() 的图象经过定点
的图象经过定点![]()
要使两个函数有两个交点,一次函数![]() 经过点
经过点![]() 是一个临界位置,此时有
是一个临界位置,此时有![]() ,即
,即![]()
因此,结合函数图象可知,当![]() 时,两个函数必有两个交点,即关于
时,两个函数必有两个交点,即关于![]() 的方程
的方程![]() 有两个不相等的实数根
有两个不相等的实数根
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
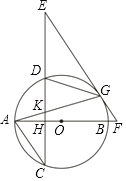
【题目】如图,AB是⊙O的直径,过圆外一点E作EF与⊙O相切于G,交AB的延长线于F,EC⊥AB于H,交⊙O于D,C两点,连接AG交DC于K.
(1)求证:EG=EK;
(2)连接AC,若AC∥EF,cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
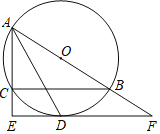
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=8,CE=4,求弧BD的长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
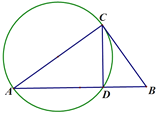
【题目】下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.

作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂尔多斯市某百货商场销售某一热销商品A,其进货和销售情况如下:用16000元购进一批该热销商品A,上市后很快销售一空,根据市场需求情况,该商场又用7500元购进第二批该商品,已知第二批所购件数是第一批所购件数的一半,且每件商品的进价比第一批的进价少10元.
(1)求商场第二批商品A的进价;
(2)商场同时销售另一种热销商品B,已知商品B的进价与第二批商品A的进价相同,且最初销售价为165元,每天能卖出125件,经市场销售发现,若售价每上涨1元,其每天销售量就减少5件,问商场该如何定售价,每天才能获得最大利润?并求出每天的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com