
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上的两个点,且
上的两个点,且![]() ,
,![]() ,则
,则![]() 的外接圆的半径是________.
的外接圆的半径是________.

【答案】![]()
【解析】
设∠DCE=x,∠ACD=y,根据等腰三角形的性质求出∠ACE、∠BDC,根据三角形内角和定理求出∠DCE=45°,根据三角形的外接圆和外心的概念求出答案.

设∠DCE=x,∠ACD=y,则∠ACE=x+y,∠BCE=90°∠ACE=90°xy,
∵AE=AC,
∴∠ACE=∠AEC=x+y,
∵BD=BC,
∴∠BDC=∠BCD=∠BCE+∠DCE=90°xy+x=90°y,
在△DCE中,∵∠DCE+∠CDE+∠DEC=180°,
∴x+(90°y)+(x+y)=180°,
解得x=45°,
∴∠DCE=45°,
∵AC=6,BC=8,
∴AB=![]() =10,
=10,
∵AE=AC=6,BD=BC=8,
∴DE=4,又∠DCE=45°,
如图,作直径CH,连接HE,
∴∠CEH=90°,又∠CHE=∠DCE=45°,CE=4,
∴CH=4![]() ,
,
即△DCE的外接圆的直径4![]() ,
,
∴△DCE的外接圆的半径为2![]() .
.


科目:初中数学 来源: 题型:
【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.在抛物线y=ax2+bx+c中,系数a、b、c为绝对值不大于1的整数,则该抛物线的“抛物线三角形”是等腰直角三角形的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:
,其部分图象如图所示,下列结论:
①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ③
③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大
增大而增大
其中结论正确的个数是( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
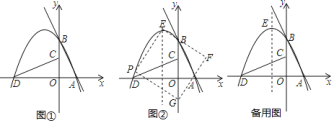
【题目】如图①,若直线![]() 交
交![]() 轴于点
轴于点![]() 、交
、交![]() 轴于点
轴于点![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .过点
.过点![]() ,
,![]() ,
,![]() 的抛物线
的抛物线![]() .
.
![]() 求抛物线
求抛物线![]() 的表达式;
的表达式;
![]() 若与
若与![]() 轴平行的直线
轴平行的直线![]() 以
以![]() 秒钟一个单位长的速度从
秒钟一个单位长的速度从![]() 轴向左平移,交线段
轴向左平移,交线段![]() 于点
于点![]() 、交抛物线
、交抛物线![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值;
的最大值;
![]() 如图②,点
如图②,点![]() 为抛物线
为抛物线![]() 的顶点,点
的顶点,点![]() 是抛物线
是抛物线![]() 在第二象限的上一动点(不与点
在第二象限的上一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() .随着点
.随着点![]() 的运动,正方形的大小、位置也随之改变,当顶点
的运动,正方形的大小、位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,直接写出对应的点
轴上时,直接写出对应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
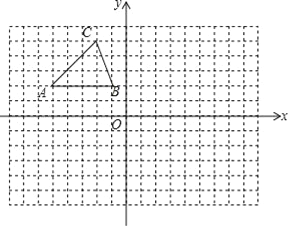
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com