
【题目】如图,已知![]() 和
和![]() 均为的等边三角形,点
均为的等边三角形,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 与
与![]() 平行的直线交射线
平行的直线交射线![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() ,
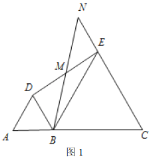
,![]() 三点在同一直线上时(如图1),求证:
三点在同一直线上时(如图1),求证:![]() 为
为![]() 中点;
中点;
(2)将图1中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() ,
,![]() ,
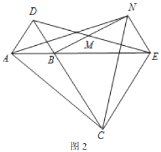
,![]() 三点在同一直线上时(如图2),求证:
三点在同一直线上时(如图2),求证:![]() 为等边三角形;
为等边三角形;
(3)将图2中![]() 绕点
绕点![]() 继续顺时针旋转多少度时,点
继续顺时针旋转多少度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,试作出图形并直接写出
中点,试作出图形并直接写出![]() 绕点
绕点![]() 继续旋转的度数.
继续旋转的度数.
【答案】(1)见解析;(2)见解析;(3)![]() 绕点
绕点![]() 继续顺时针旋转30度时,点
继续顺时针旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点
中点
【解析】
(1) 根据![]() ,点
,点![]() 为
为![]() 的中点,可证明
的中点,可证明![]() ,从而
,从而![]() ,可得到答案;
,可得到答案;
(2) 先证明![]() ,得到
,得到![]() ,再证
,再证![]() 由一个角是60°,即证明
由一个角是60°,即证明![]() 是等边三角形;
是等边三角形;
(3) 先证明![]() ,证
,证![]() ,得到
,得到![]() 是等边三角形,再利用点
是等边三角形,再利用点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,可得到答案.
中点,可得到答案.
证明:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
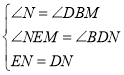
∴![]() ,
,
∴![]() ,即
,即![]() 为
为![]() 中点.
中点.
(2)∵![]() ,
,
∴![]() ,(1)中已经证明,
,(1)中已经证明,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 三点在同一直线上,
三点在同一直线上,
∴![]() ,
,
∵![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
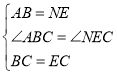
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() 为等边三角形(由一个角是60°的等腰三角形是等边三角形).
为等边三角形(由一个角是60°的等腰三角形是等边三角形).
(3)如图,当![]() 绕点
绕点![]() 继续旋转时,点
继续旋转时,点![]() 在线段
在线段![]() 上.
上.
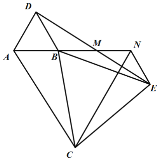
![]() 绕点
绕点![]() 继续旋转30度时,点
继续旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点.
中点.
(附理由:∵![]() ,
,
∴![]() (1)中已经证明,
(1)中已经证明,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() 为等边三角形.
为等边三角形.
∴当点![]() 恰好位于线段
恰好位于线段![]() 中点时,
中点时,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
即![]() 绕点
绕点![]() 继续顺时针旋转30度时,点
继续顺时针旋转30度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点.
中点.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】我市公交总公司为节约资源同时惠及民生,拟对一些乘客数量较少的路线换成中巴车.该公司计划购买![]() 台中巴车,现有甲、乙两种型号,已知购买一台甲型车比购买一台乙型车少
台中巴车,现有甲、乙两种型号,已知购买一台甲型车比购买一台乙型车少![]() 万元,购买
万元,购买![]() 台甲型车比购买
台甲型车比购买![]() 台乙型车多
台乙型车多![]() 万元.
万元.
(1)问购买一台甲型车和一台乙型车分别需要多少万元?
(2)经了解,每台甲型车每年节省费用![]() 万元,每台乙型车每年节省费用
万元,每台乙型车每年节省费用![]() 万元,若要使购买的这批中巴车每年至少能节省
万元,若要使购买的这批中巴车每年至少能节省![]() 万,则购买甲型车至少多少台?
万,则购买甲型车至少多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
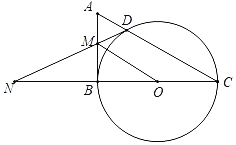
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了加强和改进学校体育工作,切实提高学生体质健康水平,决定开展“阳光体育”活动,现对全校学生感兴趣的球类项目(![]() 表示足球,
表示足球,![]() 表示篮球,
表示篮球,![]() 表示排球,
表示排球,![]() 表示羽毛球,
表示羽毛球,![]() 表示乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,张老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(部分信息未给出).
表示乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,张老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(部分信息未给出).
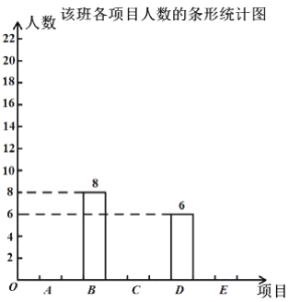
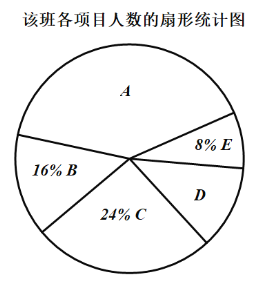
(1)求该班级学生的总人数;
(2)将条形统计图补充完整;
(3)若该校共有学生1500名,请估计有多少人选修足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
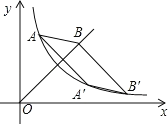
【题目】如图,已知反比例函数y=![]() (x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A'(4,b)与点B'均在反比例函数的图象上,点B在直线y=x上,四边形AA'B'B是平行四边形,则B点的坐标为______.
(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A'(4,b)与点B'均在反比例函数的图象上,点B在直线y=x上,四边形AA'B'B是平行四边形,则B点的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
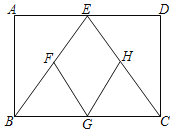
【题目】如图,已知四边形ABCD是矩形,点E,G分别是AD,BC边的中点,连接BE,CE,点F,H分别是BE,CE的中点连接FG,HG.
(1)求证:四边形EFGH是菱形;
(2)当![]() = 时,四边形EFGH是正方形.
= 时,四边形EFGH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
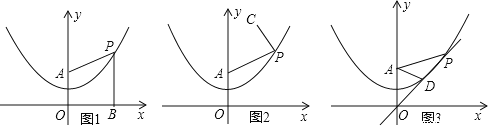
【题目】已知,在平面直角坐标系xOy中,点A的坐标为(0,2),点P(m,n)是抛物线![]() 上的一个动点.
上的一个动点.
(1)如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PA_____PB(直接填写“>”“<”或“=”,不需解题过程);
(2)请利用(1)的结论解决下列问题:
①如图2,设C的坐标为(2,5),连接PC,AP+PC是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,将
上,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() .
.
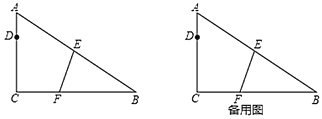
(1)求![]() 的长;
的长;
(2)点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
①当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ________;
________;
(3)将直线![]() 平移,平移后的直线与直线
平移,平移后的直线与直线![]() ,直线
,直线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,以线段
,以线段![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧,连接
两侧,连接![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com