
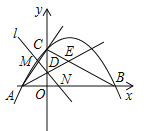
【题目】(2017南宁,第26题,10分)如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
【答案】(1)a=![]() ,A(﹣
,A(﹣![]() ,0),抛物线的对称轴为x=
,0),抛物线的对称轴为x=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,0)或(
,0)或(![]() ,﹣4);(3)
,﹣4);(3)![]() .
.
【解析】试题分析:(1)由点C的坐标为(0,3),可知﹣9a=3,故此可求得a的值,然后令y=0得到关于x的方程,解关于x的方程可得到点A和点B的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;
(2)利用特殊锐角三角函数值可求得∠CAO=60°,依据AE为∠BAC的角平分线可求得∠DAO=30°,然后利用特殊锐角三角函数值可求得OD=1,则可得到点D的坐标.设点P的坐标为(![]() ,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
(3)设直线MN的解析式为y=kx+1,接下来求得点M和点N的横坐标,于是可得到AN的长,然后利用特殊锐角三角函数值可求得AM的长,最后将AM和AN的长代入化简即可.
试题解析:(1)∵C(0,3),∴﹣9a=3,解得:a=![]() .
.
令y=0得:![]() ,∵a≠0,∴
,∵a≠0,∴![]() ,解得:x=﹣
,解得:x=﹣![]() 或x=
或x=![]() ,∴点A的坐标为(﹣
,∴点A的坐标为(﹣![]() ,0),B(
,0),B(![]() ,0),∴抛物线的对称轴为x=
,0),∴抛物线的对称轴为x=![]() .
.
(2)∵OA=![]() ,OC=3,∴tan∠CAO=
,OC=3,∴tan∠CAO=![]() ,∴∠CAO=60°.
,∴∠CAO=60°.
∵AE为∠BAC的平分线,∴∠DAO=30°,∴DO=![]() AO=1,∴点D的坐标为(0,1).
AO=1,∴点D的坐标为(0,1).
设点P的坐标为(![]() ,a).
,a).
依据两点间的距离公式可知:AD2=4,AP2=12+a2,DP2=3+(a﹣1)2.
当AD=PA时,4=12+a2,方程无解.
当AD=DP时,4=3+(a﹣1)2,解得a=0或a=2(舍去),∴点P的坐标为(![]() ,0).
,0).
当AP=DP时,12+a2=3+(a﹣1)2,解得a=﹣4,∴点P的坐标为(![]() ,﹣4).
,﹣4).
综上所述,点P的坐标为(![]() ,0)或(
,0)或(![]() ,﹣4).
,﹣4).
(3)设直线AC的解析式为y=mx+3,将点A的坐标代入得:![]() ,解得:m=
,解得:m=![]() ,∴直线AC的解析式为
,∴直线AC的解析式为![]() .
.
设直线MN的解析式为y=kx+1.
把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,∴点N的坐标为(
,∴点N的坐标为(![]() ,0),∴AN=
,0),∴AN=![]() =
=![]() .
.
将![]() 与y=kx+1联立解得:x=
与y=kx+1联立解得:x=![]() ,∴点M的横坐标为
,∴点M的横坐标为![]() .
.
过点M作MG⊥x轴,垂足为G.则AG=![]() .
.
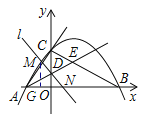
∵∠MAG=60°,∠AGM=90°,∴AM=2AG=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知:方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图:
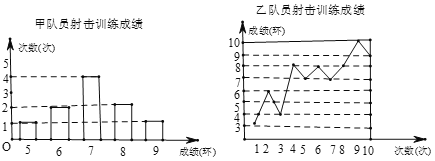
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差( | |
甲 | 7 |
| 7 | 1. 2 |
乙 |
| 7. 5 |
| 4. 2 |
(1)分别求表格中![]() 、
、![]() 、
、![]() 的值.
的值.
(2)如果其他参赛选手的射击成绩都在7环左右,应该选______队员参赛更适合;如果其他参赛选手的射击成绩都在8环左右,应该选______队员参赛更适合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人分别骑自行车和摩托车从![]() 地出发前往
地出发前往![]() 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数图象如图所示.
之间的函数图象如图所示.

(1)甲骑自行车的速度是_____![]() .
.
(2)求乙休息后所行的路程![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过![]() .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数对应的点沿数轴向右平移
,再把所得数对应的点沿数轴向右平移![]() 个单位长度,得到点
个单位长度,得到点![]() .称这样的操作为点
.称这样的操作为点![]() 的“倍移”,对数轴上的点
的“倍移”,对数轴上的点![]() ,
,![]() ,
, ![]() ,
,![]() 进行“倍移”操作得到的点分别为
进行“倍移”操作得到的点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,
时,
①若点![]() 表示的数为
表示的数为![]() ,则它的对应点
,则它的对应点![]() 表示的数为 .若点
表示的数为 .若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数为 ; ②数轴上的点
表示的数为 ; ②数轴上的点![]() 表示的数为1,若
表示的数为1,若![]() ,则点
,则点![]() 表示的数为 ;
表示的数为 ;
(2)当![]() 时,若点
时,若点![]() 表示的数为
表示的数为![]() ,则
,则![]() 的值为 ;
的值为 ;
(3)若线段![]() ,请写出你能由此得到的结论.
,请写出你能由此得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
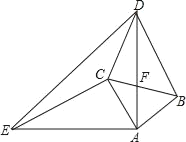
【题目】如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC=2![]() ,求∠ACD的度数;
,求∠ACD的度数;
(3)在(2)的条件下,直接写出DE的长为 .(只填结果,不用写计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
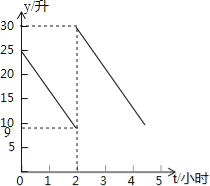
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
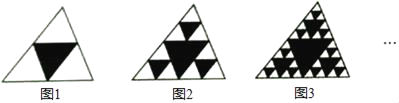
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com