
【题目】如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①DE=DF;
②∠EDF=90°;
③四边形CEDF不可能为正方形;
④四边形CEDF的面积保持不变.
一定成立的结论有(把你认为正确的序号都填上)
【答案】①②④
【解析】解:①连接CD;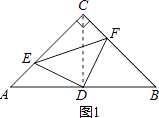
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE和△CDF中,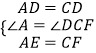
∴△ADE≌△CDF(SAS),
∴ED=DF,①正确;
②∵△ADE≌△CDF,
∴∠CDF=∠EDA,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,②正确;
③当E、F分别为AC、BC中点时,DE⊥AC,DF⊥BC,又∠ACB=90°,
∴四边形CEDF是矩形,
∵CE=CF,
∴四边形CDFE是正方形,③错误;
④如图2,分别过点D,作DM⊥AC,DN⊥BC,于点M,N,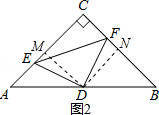
则DM=DN,
在Rt△DME和Rt△DNF中,![]() ,
,
∴Rt△DME≌Rt△DNF(HL),
∴四边形CEDF的面积等于正方形CMDN面积,故面积保持不变,④正确,
所以答案是:①②④.
【考点精析】掌握等腰三角形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.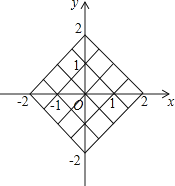
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:
若二次三项式x2-4x+m有一个因式是x+3,求另一个因式及m的值.
解:设另一个因式为x+a
则x2-4x+m=(x+3)(x+a)=x2+ax+3x+3a=x2+(a+3)x+3a,
∴![]() ∴
∴![]()
∴另一个因式为x-7,m的值为-21.
请依照以上方法解答下面问题:
(1)已知二次三项式x2+3x-k有一个因式是x-5,求另一个因式及k的值;
(2)已知二次三项式2x2+5x+k有一个因式是x+3,求另一个因式及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( ![]() )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( ![]() )海里.
)海里.
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(参考数据: ![]() =1.41,
=1.41, ![]() =1.73,
=1.73, ![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论: ①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0; 其中正确的结论有( )
A.1 个
B.2 个
C.3 个
D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①下午 2 点 10 分时,钟表的时针和分针所成锐角是________;
②如图,射线 OC,OD 在∠AOB 的内部,射线 OM,ON 分别平分∠AOD,∠BOC, 且∠BON=50°,∠AOM=40°,∠COD=30°,则∠AOB 的度数为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠BDE=2∠BCE.其中正确结论的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式
12=1= ![]() ×1×2×(2+1)
×1×2×(2+1)
12+22= ![]() ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ![]() ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ![]() ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板的一边ON与射线OB重合,过点O在三角板的内部,作射线OC,使∠NOC:∠MOC=2:1,求∠AOC的度数;
(2)如图2,将三角板绕点O逆时针旋转一定角度到图2的位置,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB对的角平分线,此时∠AOM与∠NOC满足怎样的数量关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com