
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,下列四个结论:
,下列四个结论:
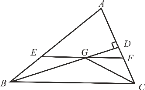
①![]() ; ②
; ②![]() ;
;
③点![]() 到
到![]() 各边的距离相等;
各边的距离相等;
④设![]() ,
,![]() ,则
,则![]() .
.
其中正确的结论有( )
A.①②④B.①②③C.①③④D.①②③④
【答案】B
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点G,根据角平分线的定义与三角形内角和定理,即可求得②∠BGC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEG和△CFG是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点G到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设GD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEG和△CFG是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点G到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设GD=m,AE+AF=n,则S△AEF=![]() mn,故④错误.
mn,故④错误.
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴∠GBC=![]() ∠ABC,∠GCB=
∠ABC,∠GCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠GBC+∠GCB=90°-![]() ∠A,
∠A,
∴∠BGC=180°-(∠GBC+∠GCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴∠GBC=∠GBE,∠GCB=∠GCF,
∵EF∥BC,
∴∠GBC=∠EGB,∠GCB=∠FGC,
∴∠EGB=∠GBE,∠FGC=∠GCF,
∴BE=GE,CF=GF,
∴EF=GE+GF=BE+CF,
故①正确;
过点G作GM⊥AB于M,作GN⊥BC于N,连接GA,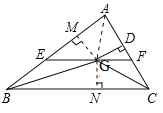
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴GN=GD=GM=m,
∴S△AEF=S△AGE+S△AGF=![]() AEGM+
AEGM+![]() AFGD=
AFGD=![]() GD(AE+AF)=
GD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴点G到△ABC各边的距离相等,故③正确.
故选:B.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共![]() 个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
![]() 请估计:当
请估计:当![]() 很大时,摸到白球的频率将会接近于多少?
很大时,摸到白球的频率将会接近于多少?
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的概率 |
|
|
|
|
|
|
![]() 假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
![]() 试估算口袋中黑、白两种颜色的球各有多少个?
试估算口袋中黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图,点M是正方形ABCD的边BC上一点,点N是CD延长线上一点,且MA⊥AN,易证△ABM≌△ADN,进而证得∠AMB=∠AND.
(应用)如图(1),在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°.求证:∠BEA=∠AEF.
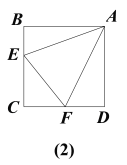
(拓展)如图(2),在四边形ABCD中,AB=AD,∠BAD=90°,∠B+∠D=180°,点E,F分别在边BC、CD上,∠EAF=45°.若∠BEA=50°,则∠AFD的大小为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 边
边![]() ,
,![]() 上的两个动点,其中点
上的两个动点,其中点![]() 以每秒2个单位的速度由点
以每秒2个单位的速度由点![]() 向点
向点![]() 运动;点
运动;点![]() 以每秒3个单位的速度由点
以每秒3个单位的速度由点![]() 到点
到点![]() 再到点
再到点![]() 运动;它们同时出发,当一个点到达终点停止,另一个点继续运动到终点也停止,设运动时间为
运动;它们同时出发,当一个点到达终点停止,另一个点继续运动到终点也停止,设运动时间为![]() 秒。
秒。
(1)求![]() 的面积。
的面积。
(2)当点![]() 在边
在边![]() 上运动时,出发几秒后,
上运动时,出发几秒后,![]() 是等腰三角形。
是等腰三角形。
(3)当点![]() 在边
在边![]() 上运动时,出发几秒后,
上运动时,出发几秒后,![]() 是等腰三角形。
是等腰三角形。
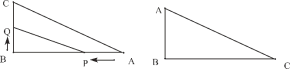
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com